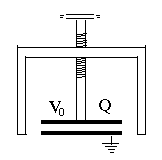
(E18) Pumping up the Voltage of a Static ChargeThe two short formulas lead to some interesting consequences. Imagine the apparatus schematically drawn on the right, a capacitor with variable separation. A grounded conducting frame (black) holds at one end a round metal plate, with a similar plate facing it some distance above it, mounted at the end of a long insulating screw which allows the separation between the plates to be adjusted. We start with the plates close to each other, forming a parallel plate capacitor of capacitance C0. From some source--e.g. static friction--an electric voltage generator or even a large battery--we charge the movable plate to a voltage +V0 relative to the ground (and to the other plate). From our formulas, the plate now carries a positive charge Now turn the screw to increase the separation D between the plates 10 times. Since the capacitance of a parallel plate capacitor (for small separations only) is inversely proportional to D --that is, it is proportional to 1/D -- the new capacitance is 10 times smaller: However the electric charge has nowhere to go--so as before, it remains Q0. Therefore, to preserve the relation with Q = Q0 the voltage must increase 10-fold: Pulling back the plate pumps up the voltage! There is even more surprise when we calculate the energy The stored electrical energy has also increased 10-fold! Have we perhaps discovered a source of boundless electrical energy? No such luck! Energy must still be conserved, or as the saying goes, "no such thing as a free lunch". Since the two plates carry charges of opposite sign, they attract each other, and when pulling them apart, we must overcome that attraction. That means we must perform mechanical work, and invest energy from some other source. It all balances, and putting a dielectric layer in between only increases the effect, because the initial electric charge can be larger.
The Electrophorus (optional addition)The above result is a general one: by overcoming electrical attraction of charges by increasing their separation, we boost the voltage. When drying garments made of artificial fibers (nylon, rayon etc.) in a clothes dryer, friction does charge them up electrically and makes them cling together. But the voltage really increases, to where sparks may crackle, only when you pull them apart!An apparatus for producing high voltages by separating electrical charges separated by an insulator was the electrophorus devised by the Italian Alessandro Volta in 1775. It was the same Volta who later went on to invent the "voltaic pile," the first electrical battery. The device consisted of two round conducting plates of the same size, insulated from their surroundings and separated by a thin insulator. The lower one lies on a table (insulated from it) and the top one had an insulating handle, by which it can be placed above the bottom plate, separated by insulator. The name "electrophorus" means carrier of electricity, which was the purpose of the apparatus. Say you have an insulated metal ball you want to charge electrically (balls and rounded objects work best in keeping charge from escaping, whereas sharp points build up the local electric force and tend to leak charge). You can charge it by touching it with some charged object held by an insulating handle; but after you have done so, what next? The ball is charged and you can only add charge from an object with higher voltage. A fluid flows only from high pressure to lower one, and electricity acts that way, too. With an electrophorus, however, you can charge it again and again. 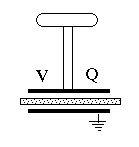
We do best without the frame and screw: just two plates, separated by some dielectric insulator, with an insulated handle.
Put the top plate back on the insulator. It now has less charge, since some was passed to the ball. However, the charge –Q on the bottom again induces a charge separation in the top (see preceding section). The separated negative charge on top can be removed by grounding, leaving again +Q on the top plate. Now the process can be repeated, again and again. It only slows down when the voltage of the ball approaches the one of the lifted electrophorus. 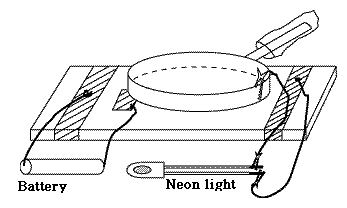
As a fun experiment, I once constructed an electrophorus using kitchen equipment and a neon lamp (also wires and alligator clips, though bare paper clips might also work). It raised the voltage of an electric cell (1.5 volt) sufficiently to cause the neon lamp to blink, although that only happens with voltages around 70v. In the kitchen you can find good insulators (polyethylene and saran wrap) and good conductors (aluminum foil), and the lifted plate was a large frying pan. You can read about it here. If you can get a bare neon bulb (instead of one protected by a resistance) you will probably get a brighter flash. Other examples of Static ElectricitySimilarly, when a xerographic copier ("xerox machine") is used for copying printed material onto transparent acetate sheets used by projectors, such sheets get charged electrically by the printing process. If you stack them as they come out of the machine, they will cling together, and the static cling only gets worse if you pry them apart, because again, you are raising the voltage. Much better to lay them down separately as they come out, letting them cool off and letting the charge leak away, then bringing them together only afterwards.
A little further in the rotation, the pattern to be printed is projected onto the disk, either from a light that scans the document to be copied or (in a laser printer) from a computer-controlled laser (or else, from an array of light-emitting diodes). The light removes the charge from all areas expected to remain white. The drum continues to turn to where its dark parts, still charged, attract particles of a fine carbon powder. Then a bit further still, that powder is deposited on paper, and a heating element melts some glue-like material ("fuser" or "dry ink") in the powder, causing it to stick to the page. Finally, all remaining charge is removed--works with paper but less so with acetate sheets. Both are described in a section of the collection "From Stargazers to Starships," in the section "Work against an Electric Force: the Van De Graaff generator." |