(E24) Induction and Magnetic FluxThe Electro-Motive ForceRepeating earlier definitions: a vector field is just a region in space where every point is associated with some vector (to a mathematician the term "vector field" may have additional meanings). In a gravitational field each point is associated with a vector giving the local force (G?) on one kilogram of mass. Wherever you may be now, it probably points straight down to the center of the Earth!In a magnetic field each point is associated with the local force B on a unit m of magnetic polarity (however we define it). As the compass needle shows, these vectors diverge from the southern polar region and converge in the northern polar region, where they point nearly vertically, though how they continue underground is not observable. And in an electric field at any point, the field vector E gives the force on one coulomb of electric charge, if placed at that point. The expectation of "if placed" can in each case be inferred from observations elsewhere and physical laws. The study of fluids suggest yet another "field": given a large volume of fluid in which with a pattern of flows exists, each point is associated with some flow velocity field v. Such flows can be complex and even unstable (breaking up into turbulence) and their laws depend on whether the fluid is compressible (like air) or not (like water, almost incompressible). Since the 1700s, a great amount of study has targeted the behavior of such "flow fields", including the recent fashion of simulation by large computers, and though such fields may be easier to observe (e.g. by smoke in wind tunnels or sawdust suspended in water), many unanswered questions remain.
To calculate the flux, imagine dividing the surface divited into a large number of little areas (see drawing). At each area dA, we find the velocity v of the water through it (which is a vector), and find the component perpendicular to the are vperp. Each second, the volume crossing dA is a box-shaped volume with base dA and height vperp. Sum them up--we can use a computer for that, or if some mathematical law governs v and S, a suitable formula--and we have the flux of water through the contour S But which surface spanning S should be subdivided? A thin rubber membrane spanning the closed contour could be stretched into many different shapes (two are indicated in the drawing, S1 and S2). The answer is, that as long as there exist no "sources or sinks" in the volume discussed--no spouts, no drains--it makes no difference. Whatever flow through S1 must also flow through S2. The flux is the same through any such surface (as long as the fluid is incompressible). Why bring the flow of incompressible water into a discussion of magnetic fields? Because mathematically they have very similar behavior. One can define streamlines of v which at any point give the direction of the flow, and they behave very much like field lines of some magnetic field B (all this in "empty space" devoid of magnetic materials). And just as we can define the flux of v through some closed contour S, we can define the magnetic flux Φ (capital Greek F or "phi") through it too. Old texts sometimes refer to it as the "number of field lines crossing S" and that was how Faraday interpreted it, but here the concept of magnetic flux will be the same as that of James Clerk Maxwell, who continued Faraday's work Back to electromagnetic inductionFaraday found that the induced e.m.f. was only created when conditions changed. A coil and a magnet at rest generate no induced e.m.f.. However, move the coil relative to the magnet--or the magnet relative to the coil--or if it is a electromagnet, vary the intensity of the magnetic field by changing the current producing it--in all these cases an e.m.f will usually result. Faraday's law of induction in all such cases is The direction of the emf is always such that if a closed conducting wire follows the contour S, the magnetic field produced by the induced current opposes the one existing. It is as if nature opposes the change; in this case this is known as Lenz'es Law The MagnetoFor instance, if a bar magnet rotates around a shaft as drawn, and the two coils are connected so that the magnetic flux through them adds up (rather than canceling!), then Φ reverses each half turn, causing an e.m.f. in opposite directions. Halfway between these positions the magnet is perpendicular to the axis of the coils, its field lines skim parallel to the planes of the winding and the total flux through them is zero. 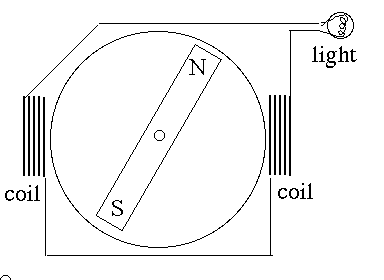
Such a simple generator of electricity is known as a magneto. It is not particularly efficient but is simple and very reliable--which is why bicycle lamps used to get power from a magneto mounted on the "fork" next to the front wheel, rotated by a wheel rubbing against the front tire. Today's bicycles prefer batteries, because with a magneto the e.m.f. and the brightness of the light depend on the speed of the wheel. Note that the rotation of a magneto generates an alternating current (AC). One reason AC is used in our homes is that it is easier to generate: even automobiles generate AC by an "alternator" and later "rectify" it using solid state diodes (described earlier) and use it for charging the battery. Of course, AC also allows the voltage to be stepped up for efficient long-distance transmission. In all this, note that a magneto must abide by the conservation of energy. Turning its "rotor" generates an electric current, flowing in coils whose magnetic force opposes the motion. Overcoming that resistance requires energy, provided by the wheel touching the front tire. A different kind of magneto is found in small gas engines, such as those of lawnmowers. The engine gets its power from a piston pushed when a mixture of air and gasoline vapor ignites rapidly and heats up. The heated expanding gas pushes the piston down a metal cylinder and in the process turns a crankshaft. The top of the cylinder also has two openings controlled by mushroom-shaped valves--one to admit fresh air-vapor mixture, the other to let out the hot burned products. The turning of the crankshaft typically cycles the engine through four "strokes" (two-stroke engines exist, but their modified cycle is less efficient). First the piston rises, the exhaust valve is open and burned gas from the preceding cycle (carbon dioxide and steam) is pushed out. Next the exhaust valve closes and the intake valve opens, and the piston descends as it sucks in a mixture of air and fuel. In the third stroke both valves close and the piston rises again, compressing the fuel mixture. Then when compression is greatest, an electric spark from an insulated "spark plug" ignites the mixture, and its heating pushes the piston in the "power stroke" (Demonstration here). Electricity is required only at one brief instant in the cycle, but at a high voltage, about 20,000 volts, to break down the resistance of the gas in the small gap between the twin contacts inside the spark plug. The plug is therefore connected to a coil (with additional components, including a switch and a high-voltage transformer), while the flywheel of the mower carries a permanent magnet, which each turn whizzes by the coil and induces the necessary voltage. Car engines operate on the same cycle, but have several cylinders and a more complex electrical system. Engines on small airplanes, however, often use magnetos, deemed more reliable. Old style telephones (also old military field phones) included a crank which the caller turned, activating a magneto which rang a bell at the other end.
|
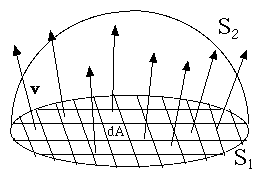 Let us concentrate on water, assuming it to be incompressible and assuming its 3-dimensional velocity v is known at any location and any time. If we imagine a thin wire following some closed loop S ("closed contour"), we can (in principle) calculate how many liters of water cross the surface spanned by of S each second. That would be the flux
(of water) through S.
Let us concentrate on water, assuming it to be incompressible and assuming its 3-dimensional velocity v is known at any location and any time. If we imagine a thin wire following some closed loop S ("closed contour"), we can (in principle) calculate how many liters of water cross the surface spanned by of S each second. That would be the flux
(of water) through S.