(E26) AC Impedance
Going Beyond Ohm's LawWith alternating current (AC), what happens to Ohm's Law? For pure resistors (e.g. those in simple bread toasters) Ohm's law is the same for both AC and DC currents, with the usual caution that here is not a fundamental law of nature, just an approximation which holds for certain materials and conditions. Fluorescent lamps don't go by it, and even the filament of a flashlight bulb increases its resistance fivefold when glowing (which helps switch it on quickly, because the initial current is 5 times larger). Nonlinear elements which protect computer power inputs don't obey Ohm's law, either: in usual operation, they act like insulators, but their insulation collapses when a large voltage spike occurs (e.g. when lightning hits a power line), protecting the device.With AC currents resistors obey Ohm's law, but in addition, new circuit elements also appear, in particular capacitors and inductors (magnetic coils, including transformers). As already noted, a capacitor will let a varying voltage pass through it. If a positive voltage rises on one plate or set of plates in the capacitor, the other plate will at first match it with an equal rise (until enough current has flowed to charge the capacitor). This makes the current effectively go through, and with AC such variations occur all the time. A capacitor's ability to transmit AC voltage depends on the speed of variation: radio-wave frequency are transmitted quite easily, sometimes even unintentionally when circuits operate close to each other (your computer probably shields some of them inside grounded aluminum boxes, to block such "pick-up"). House-current AC varies relatively slowly, 60 cycles per second, and uses larger capacitors--but smaller ones serve aboard ships and airplanes, with 400-cycle AC. Constant voltages of steady DC are, of course, completely blocked. Radians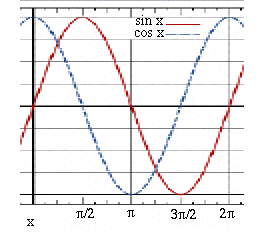
A "simple" AC voltage rises and falls in a wave like a the trigonometric sine function (red) or cosine function (blue, differing only by a horizontal shift). A location on the wave at any instant is called the AC phase (x in the graph) and is often measured in degrees, 360° for a full cycle, a system inherited from ancient Babylonians, who noted that the position of the Sun in the sky, (relative to the background stars), makes each year a full circle and advances each day about one degree. Then if f is the AC frequency in cycles per second, during a time t the functions
go each second through f cycles. In mathematics, however, angles are frequently measured in radians, units equal to about 57°. One full rotation contains 2 π radians, where π=3.1415926... is the ratio between the circumference of a circle and its diameter (yes, I have a super motorbike to travel about the roads foolishly...). It may seem strange to measure angles in units of which the circle does not even contain a whole number and which can only be used to some approximation. However, radians have mathematical advantages, e.g. formulas such as where 3!=6 ("three factorial") is produced by multiplying all integers up to 3, also 5!=120 by multiplying up to 5, and so on. That formula holds in radians; in texts using degrees, each x on the right must be multiplied by 2π/360. Following most texts, we work here in radians (except that phase angles are sometimes given in degrees), and in place of the frequency f cycles-per-second, use the "angular frequency" ω = 2 π f radians-per-second, denoted by the lower-case Greek letter omega (upper case Ω is used for "ohms"). AC Impedance--CapacitorsA capacitor of C farad with charge Q coulomb stores electric energyThe necessity to "load up" the charge in the beginning of the AC cycle (when the sine function starts fom zero) and then "unload" it again impedes the flow of current. Circuit analysis therefore includes an impedance A capacitor with large plates (and large C) has a smaller impedance, since it lets AC pass more easily--if a positive charge is added on one plate, a corresponding charge quickly accumulates on the other plate, even at moderate voltage changes, and the voltage signal continues on the other side. And the impedance of a capacitor decreases as the angular frequency ω grows, meaning a higher frequency can more easily propagate through space than a lower one. Steady DC with ω=0 cannot propagate at all but is stopped by the capacitor, which for DC is just a break in the continuity of the circuit. AC Impedance and Admittance--Inductors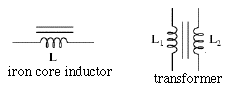
An opposite behavior is observed in current carrying coils, where every AC cycle need invest energy to build up a magnetic field, only getting the energy back when the current drops and reverses. This energy-storing property is called inductance (or "self-inductance") and is especially noted in coils, magnets and transformers: just as capacitance stores electric energy, inductance stores magnetic energy. Its unit is named the henry
after Joseph Henry who invented the practical electromagnet, and inductances in such units are usually denoted by the capital letter L. In analogy to an earlier equation, an inductor of L henry carrying a current of I amperes stores magnetic energy
If you suddenly break a circuit which includes a large inductance, this may create a big spark from the high voltage generated by the magnetic energy, as the current tries to keep going.
The impedance of a device with stored magnetic energy (coil, electromagnet, transformer, electric motor) has the opposite frequency dependence than capacitance. It is low at low frequency--for DC, only the ohmic resistance of a coil resists the current--but gets larger the more rapid the change, e.g. the higher the frequency. Its value is
The graphic symbol for an inductance is a spiral (figure above), denoting a coil. If the spiral has a few parallel straight lines next to it, the coil has an iron or ferrite core (whose effect may vary with frequency), and two parallel coils with a bundle of straight lines in the middle to denote an iron-core electric transformer. Just as a resistance R is mirrored by conductance 1/R, so impedances have corresponding AC admittances Cω and 1/Lω . Where complications beginIt would have been nice if we could carry over all the formulas of resistor circuits to capacitors and inductors. In some simple cases, that is possible: two capacitors (C1, C2) in parallel act like a single capacitor (C1 + C2), and two inductors (L1, L2) in series are equivalent to a single one (L1 + L2). The complimentary equations also hold, but please note that capacitances in (series, parallel) add up like resistors in (parallel, series).Things grow complicated in circuits including both types, and even more if resistors are included. Impedance not only depends on angular frequency ω, it also can shift the phase of the AC wave forward or backward in time (or in angle, if you wish). The sine waves of volts and amperes may shift their starting points in the cycle and that (if the waves shift differently) reduces the power transmitted. Such shifts can be represented by replacing sin ωt with combinations of sines and cosines, or by a mathematical scheme which requires "complex numbers", a set of mathematical objects broader than "ordinary" numbers, including all of those plus "imaginary" parts proportional to multiples of i=√–1 (in texts on electricity, it is often replaced by the letter j, reserving i for current). For this introductory overview, that would be going too far; you may look up here, a file which is part of an extensive course on electricity. Let us just note that a mere shift of phase (when ohmic resistance is negligible) absorbs no energy, it just mixes up some of the waves because of temporary storage of electric energy (in capacitors) or magnetic energy (in inductors). Such combinations can serve as frequency filters, useful (for instance) when you try to tune in a radio or TV broadcast of a certain frequency while rejecting all others which are "on the air" at the same time. The Crystal RadioWhen tuning a radio, the knob which you turn is usually connected to a variable capacitor, whose symbol is a pair of parallel lines (like any capacitor) crossed by a slanted arrow. Like any capacitor, this one too has two sets of plates, separated by empty space or by an insulating "dielectric material." One set is fixed (and often grounded), while the other one is connected to the shaft of the tuning knob. By turning the knob, you change the extent to which the plates overlap--and since only the overlap (essentially) contributes capacitance--this changes the effective capacitance.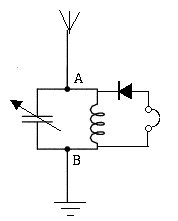 
Consider a capacitor and inductor connected "in parallel" between points A and B. If the inductor has negligible ohmic resistance, for a steady DC (ω=0) it essentially short-circuits A to B, so their voltage difference is zero. On the other hand, for DC the capacitor is an open gap and can be omitted from the circuit. Going to the other extreme, a high radio frequency (say, ten million cycles per second), the capacitor places a very low impedance between A and B--it acts like a short circuit for the radio frequency. The coil on the other hand has such high impedance that we may just as well ignore it. At these extremes of the frequency range, the impedance between A and B is near zero--like a direct connection which allows no voltage drop between those points. But not in a range of ω in-between, where both capacitance and inductance have non-zero impedance. In fact, somewhere in the middle range a resonance exists and the impedance is large, so that if B is earthed while A receives a large AC wave, an AC voltage can build up between these points. Jump ahead a few steps. Suppose A is attached to a wire in space, suspended from insulating supports and subject to whatever electric fields exist there. If the location is near a strong AM radio station, it can capture some of the radio signal. The wire then becomes a receiving antenna, marked in the diagram by several short lines forming moderate angles (like a schematic broomstick). If the variable capacitor is now adjusted so that the resonant frequency f of the circuit matches the frequency of the transmitter, the voltage of A will rise and fall with the radio signal. If the resonance is elsewhere, the impedance between A and B is small and only a small signal voltage exists between A and B.
However, we not only want to detect the radio-frequency signal, but also decode the sound signal it carries. One of the earliest methods of encoding sound was amplitude modulation (AM), taking a wave with fixed frequency and modulating its height to follow the electric signal from a microphone. Car radios still receive AM radio, and so will the outdoor antenna we described. If we now insert a solid state diode like the one converting AC to DC in section #16, the earphones may respond to the average voltage, filter away the radio frequency and leave speech or music only. You will then have created a "crystal radio" like the one built by schoolboys in the early days of radio. Reliable "solid-state rectifiers" did not yet exist, but certain crystals touched by thin wire "whiskers" had similar properties, and persistent amateurs could sometimes hear broadcasts. It wasn't a good radio receiver then, and even now, with a solid state rectifier, it performs poorly, because the earphones have no energy source except the captured part of the radio wave, which tends to be quite weak. Regular radios amplify the weak signal, using the energy of batteries or of power supplies like the one in section #16. But the crystal radio was one beginning. Radio Waves themselves will be discussed later. For now, just take for granted that all space around you contains oscillating voltages, broadcast by countless antennas in many frequencies, all over the country and the world. |