(E-6) More Resistor NetworksThe same current I flows through all of them, but the imposed voltage V is divided among the resistors in proportion to their resistance--more of it drops across the larger resistance, less across the smaller one. 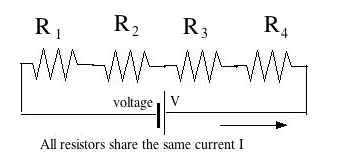
The other "standard" connection scheme of resistors is in parallel--all resistors receiving input from the same point, and supplying their current to the same point.
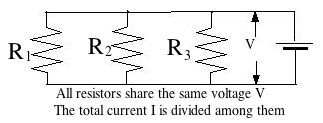
Connecting cells in parallel gives the same voltage as a single cell, but a much larger current can be extracted without an overload. However, all cells then better give the same voltage, or those producing a higher voltage will start charging those of lower voltage.)
An array of resistors in parallel
R1, R2, R3,...
may also be replaced by a single "equivalent resistance" R. Suppose we have 3 resistors. Since all are fed from the same voltage V and Ohm's law is obeyed by each, their currents are
So the total current is So, if R is the equivalent resistance of the circuit If as in the preceding section The rule is: resistances in series have an equivalent resistance larger than any of them, while resistances in parallel have an equivalent resistance smaller than any of them. Practice problems to work out:
(2) Resistors of 60Ω, 90Ω and 150Ω in parallel ... R = ? Applications
Home circuits are always wired with all outlets and connections in parallel, because each of them must be fed from the same 110v supply (220v in Europe). Suppose you wired a room for two identical filament lightbulbs, then when you switched on the circuit, both lamps lit up together (as they were supposed to)--but their filaments were dim and glowed weakly. Why? Most probably because by mistake you wired both lamps in series, not in parallel, so that the same current passed through both and each got only 55 volts. Want to be sure? Unscrew one--the other should go dark, too. Of course, the total current you can draw from a home circuit is limited. If you connect too many lights and appliances, or somehow connect wires with opposite voltages directly (a "short circuit" with very little resistance), your circuit will draw a very large electric current. As discussed later in section 8, that releases too many "watts" of electrical power in the wiring carrying the current, causing it to get dangerously hot. In most homes, a fuse or a circuit breaker (to be discussed later) then automatically disconnects the power, and the circuit will go dark. That will be your warning--before an excessive current melts your wiring, burns insulation or perhaps starts a house fire; newspaper reports of fires often end with "...the fire chief believes the fire had an electrical origin," and that is how it happens.
To derive the current drawn by a more complicated circuit, you can often start by replacing combinations of resistors with equivalent resistances. For instance, with the circuit shown here
So R4 = 4Ω and the equivalent resistance of the entire circuit is Such a situation arises with batteries and cells under heavy load. The current they supply has to overcome not only the resistance, in the external circuit but also the internal resistance Ri of the conducting liquid ("electrolyte") which closes the circuit inside the battery or cell (to be sure, this is a simplified pictures). Ri is generally small, but it sets a limit to the current which can be extracted, even when the terminals are connected directly ("shorted out").
The above circuit (conceptually, not in actual values) may be viewed as representing the circuit of a car, with R3=4Ω the internal resistance of the battery (actual value probably less), and R1=20Ω the resistance of the headlights, which draw a moderate current. Some voltage may drop while overcoming R3, but not much. However, when the electrical starter is connected (represented by R2=5Ω) the effective load with Ri=4Ω equals the internal resistance of the battery, and therefore only half the available voltage appears across the circuit AB of the headlights.
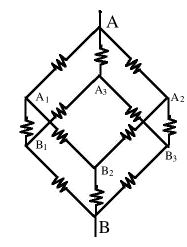
Node analysis (optional)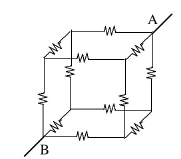
Not all resistor circuits can be resolved into combinations of resistors in parallel and in series. Consider a "classical" problem appearing in many textbooks: A 10V voltage is applied between opposite corners (A,B) of a cube consisting of 12 resistors of 1Ω each. How much current will flow--or in other words, what is the equivalent resistance R between A and B?
That method is based on the idea that in any complicated network of resistors connected to some voltage source, any nth resistor Rn, its current In and the voltage difference ΔVn between its ends (delta or Δ [capital D in Greek] generally denotes "difference") are connected by Ohm's law As long as that law holds, the resistance of an array is the same for any applied voltage, so let us assume ΔV = 10V between A and B--say V=10 at A and V=0 at B, since the choice of the point where V=0 is arbitrary. That leaves 6 corners of "nodes" where wires meet, with voltages V1, V2, V3, ... V6. The first 3 voltages will be assigned to points (A1,A2,A3) connected directly to A, the last 3 will be the voltages of (B1,B2,B3) connected directly to B There also exist 6 equations, one for each node, expressing the requirement that "what flows in equals what flows out". Six equations with 6 unknown can usually be solved: use one to express V6 in terms of the others, use the relation to replace V6 in the remaining 5 equations. Then do the same to V5 reducing the number of equations to 4, and so on, until one voltage remains, expressed by the remaining one equation. 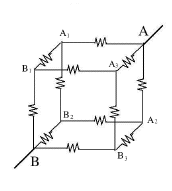
But you can also find a 3-fold symmetry. Look down diagonally down on one corner, as in the image on the right. Imagine a thin straight rod entering the cube at that point and coming out again at the most distant corner in the bottom (the rod will go through the middle of the cube). Three edges of the cube come out of that corner: if you rotate the cube around the rod by 120°, it will appear again as the one in the picture, but now the 3 edges have changed their positions. If you rotate 3 times by 120°, all edges (and other parts of the cube are back where they were at first: a 3-fold symmetry. In the cube of 12 resistors (larger drawing), let corner "A" be the corner where the rod entered, corner "B" the one where it comes out again. The rod is replaced by the conductors bringing current to A and taking it out again from B; there is no need for its middle portion and it is not drawn. At point "A" three resistors spread out symmetrically to points (A1,A2,A3). Because of the 3-fold symmetry, the positions in the circuit of the 3 resistors leading to them are completely equivalent: not only are they equal, but the current from each continues to two resistors of 1 Ω, each of which leads to one of corners (B1,B2,B3). These corners are also completely equivalent, by a similar argument. One concludes that the 3 different directions in which electric currents spread from A are completely similar. One therefore expect the 3 currents to be equal. If the current entering "A" equals I amperes, then each of these currents has intensity I/3. By Ohm's law, the voltage drop along each of the resistors connected at A is also the same, so the voltage at points (A1,A2,A3) must also be the same. We name it V1 Node B has exactly the same symmetry with respect to (B1,B2,B3), so if a current of I amperes leaves the cube from point B (it must equal the current that enters!), each resistor connected directly to it also carries a current I/3. Again, the voltages at these 3 points are expected to be the same, and we name it V2.
Finally all 6 resistors starting from points (A1,A2,A3) have the same value of resistance (=1Ω) and carry currents from voltage V1 to voltage V2. By Ohm's law, each must carry the same current, half the current entering each of these corners, which makes it equal to I/6.
Time now to collect all the information and see if we can derive from it the connection between I and V. Three currents emerge from A, each carrying 1/3 of the total current I and satisfying
(from here omit the Ω symbol). The current from A1 splits symmetrically into two equal parts, each and the same with A2 and A3. Finally, three equal currents again unite at B, each one third of the total current: One can also omit the division by 1. Adding all three equations gives If R is the equivalent resistance of the cube, Ohms law gives If all resistors were different, you would have had 6 unknown voltages (at corners A1... B3) and 6 equations involving them. Each equation would state that the sum of all currents flowing into some corner must equal the sum of those flowing out, with currents derived by Ohm's law I=ΔV/R. (If not sure if the flow is in or out, just guess one or the other; you might get a minus somewhere, but that's OK). It may take a lot more work! Puzzlers(1) What is R if we add one more 1 Ω resistor, between A2 and A3?Answer In the cube just studied, A2 and A3 have both the same voltage, namely V1. If we connected them by any resistor (of whatever value), no current would flow in it, because both ends are at the same voltage. So R remains the same, 5/6 Ω This suggests the problem could be solved even faster by a trick based on its symmetry. Since (A1,A2,A3) are all at the same voltage, we might as well connect them by a wire of negligible resistance, so in the electric circuit they become the same point--call it "C". Similarly (B1,B2,B3) are at the same voltage, may also be connected directly and be electrically the same point in the circuit--call it "D". With these shortcuts
From A to C : three 1 Ω resistors in parallel, equivalent to R1 = 1/3 Ω
(2) Suppose the three 1 Ω resistors from A to (A1,A2,A3) are replaced by 2 Ω resistors. What is R now? Equation (2) above now changes to
Multiply by 2 The other equations stay the same. Add as before The equivalent resistance is therefore 7/6 Ω. Using the shortcut described above, R1 = 2/3 Ω and the same result is obtained. |
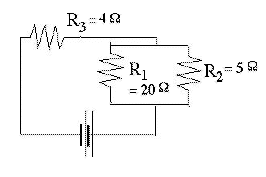 you first replace the two resistors in parallel with their equivalent single resistance R4
you first replace the two resistors in parallel with their equivalent single resistance R4