"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• How Aristarchus used the position of the half-full Moon to estimate the distance to the Sun, and the results he obtained.

• Another application of "pre-trigonometry," to a 3° triangle.

• The strange ways of scientific progress: Aristarchus made a great error--yet his final conclusion, that the Sun is much larger than Earth, still held true.

• [If (9b) is included: The fact the Sun covers a 0.5° disk in the sky means that its rays cover a cone of 0.5° opening angle, and therefore the shadow of the Earth is also such a cone.
  At points more distant than the tip of the cone, no shadow exists, for the Earth is not big enough to cover all of the Sun.]

Terms: (none new)

Stories and extras: The entire section is a story, of how Aristarchus was (probably) led to his heliocentric theory.

   The Greek philosopher Democritus argued that all matter consisted of "atoms", a Greek word meaning "undividable. " He pointed out that a collection of very small particles--e.g. sand or poppyseeds--can be poured like a continuous fluid, so maybe water, too, consists of many tiny "atoms" of water. Does this qualify as a prediction of the atomic theory of matter?

   In the early 1700s, the Irish writer Jonathan Swift wrote "Gulliver's Travels, " a satire of the politics and society of his times, in the form of voyages to distant fantastic countries (today we might have called it "science fiction.") In his third voyage he visits an island floating in the air which is ruled by an academy of scientists (a spoof on the "Royal Society", an association of Britain's top scientists which still exists). He reports that by using improved telescopes, members of the academy had discovered that two small moons orbiting Mars at a close range.

   A century and a half later, an astronomer discovered that Mars indeed had two such satellites, quite similar to what Swift had described. Does it mean that Swift had predicted those moons?

   By our standards, these are just lucky guesses. To qualify as a prediction, a claim needs not only to be stated, but also justified, it needs a logical reason. In this lesson we discuss a proposal by Aristarchus, around 270 BC, that the Earth went around the Sun, rather than vice versa. It took 1800 years before this claim was made again, and another century before it was generally accepted.

   However, this was not guesswork. Aristarchus, who also estimated the distance of the Moon, had a serious reason for his claim: the Sun, he showed, was much larger than the Earth, making it likely that the Sun, not Earth, was at the center.

   Let us go through his arguments.

Give the material of section 9a of "Stargazers. Start by assuming that the shadow of the Earth had the same width as the Earth, and that the Earth had twice the width of the Moon. Later, if time and the level of the class allow it, the teacher may continue with a discussion of the actual shadow of the Earth, which is cone-shaped [Section 9b].)

-- Who was Aristarchus of Samos?

Aristarchus was an early Greek Astronomer, living between 310-230 BC. Samos is a Greek island.
    [The teacher may point out that dates BC seem to proceed in the opposite direction to what we are used to--e.g. born -310, died -230.]

He was the first to estimate its distance, about 60 Earth radii, 380,000 km or 240,000 miles.

Two correct answers exist here:
        That the Sun was much bigger than the Earth
        That the Earth went around the Sun, not vice versa

Aristarchus tried to see where the Moon was, relative to the Sun, when it appeared to be exactly half-full.

When the Moon is half full, the angle Sun-Moon-Earth (corner at the Moon) must be exactly 90°.

You can measure that angle, for instance, if the half-moon is visible in the daytime, as often happens. It allows one to construct the full Earth-Sun-Moon triangle.

[Draw diagram of the triangle on the blackboard.]
If the Sun is very, very far away, the Sun-Earth-Moon angle is also be very close to 90°. In fact, that is the case: the amount by which that angle differs from 90° is too small to be reliably measured. The only thing one could conclude from it is that the Sun was very distant.

As it happened, the measurement made by Aristarchus was inaccurate. It is hard to tell when the Moon is exactly half full!. He believed the Sun-Earth-Moon angle was 87°, short of 90° by 3°. The Earth-Sun-Moon triangle then has a sharp corner of 3 degrees, and its proportions were such, that the Sun was about 20 times further than the Moon.

Since the Sun's size in the sky is about the same as that of the Moon, it must also be 20 times bigger in diameter.

From observation of the Earth's shadow during an eclipse of the Moon, he concluded that the Moon had half the diameter of the Earth (Actually, it is less than 1/3 that diameter). By his estimate, therefore, the Sun's diameter was 10 times that of Earth (in reality, it is more than 100 times larger).

He guessed the Earth went around the Sun, not the Sun around the Earth, as others claimed at the time, and continued to do for the next 1800 years.

   This is a detail that may be skipped in the classroom, only perhaps assigned as a project to advanced students.
   One should start it by making clear that the Sun covers a 0.5° disk of the sky. If we select some point P on Earth and trace all the sun's rays that reach it from that disk, those rays form a narrow cone.
   That cone contains all the directions in which the Sun's rays arrive at the Earth's vicinity, and the full shadow of the Earth only extends over the region where all those directions are blocked by the Earth.
   It will only extend a certain distance behind Earth. At greater distances, the Earth will cover less than 0.5° of the sky and will appear smaller than the Sun. At those distance, one can never be in the full shadow of the Earth.

"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• Understand the observed motion of the planets-- as the Sun circles the ecliptic, the inner ones move back-and-forth across the position of the Sun, while the outer ones usually advance in one direction, but with occasional temporary reversals known as "retrograde motion. "

• Understand how Hipparchus and Ptolemy explained such motions.

• Understand that from the time of Ptolemy to Copernicus, for some 1400 years, astronomy (and other sciences) in Europe saw little progress .

• Learn about the system proposed by Copernicus, and the way it explained retrograde motion: all planets moved in circles around the Sun, but the ones closer to the Sun always moved faster.

• Learn about Galileo, the first astronomer to use a telescope, and of his discoveries: the moons of Jupiter, craters on the Moon, phases of Venus (like the ones of the Moon), stars of the Milky Way.

• Learn about Galileo's defense of the Copernican theory, and the price he paid for it.

Terms: Heliocentric theory, retrograde motion, (Opposite: prograde motion), Ptolemy's theory.

Stories and extras: The theories of Ptolemy and Copernicus are briefly described. Only part of Galileo's work are covered, primarily his pioneering observations through the telescope and a brief discussion of his persecution.

   The ancient Greeks and Copernicus each had an explanation of sorts, for the way the planets appeared to be moving in the sky. But there was a big difference.

   On one hand, you had Ptolemy's theory: that is what it is called today, because it came to us through the works of Claudius Ptolemy, though it was actually Hipparchus who proposed it. Hipparchus assumed all celestial objects revolved around Earth. After all, for one such object--the Moon--that motion could actually be proved. In hindsight, it was just too bad that it was the only object that did so!

   Some of these planets seemed to go around the Sun, but others moved in strange ways, in "epicycles" around points which went around the Earth, the way the Sun was supposed to do. It was an attempt to predict where the planets would be but not to explain the motion. There was no scale we could put on the solar system--the theory gave no idea what the solar system really looked like.

   Copernicus, presented a logical picture of what the solar system looked like. The claim that all planets revolved around the Sun, and that the Earth was just one of those planets, a sphere that revolved around its axis, gave a way of predicting where the planets would be at any time.

   The idea that the Earth was not the center of the universe was opposed by many religious authorities. Copernicus therefore had to claim that he was proposing "a simpler way of predicting the positions of the planets, " not necessarily a different world-system. But actually it was much more than a prediction method.

   We like our physical theories to give us a logical picture, not just a mathematical solution. Among other things, such a picture allows us to understand intuitively the processes that are taking place.

The teacher may or may not add the following thought:

   In this course about astronomy and space, dealing with large objects moving in space, we will try to provide you, the students, with such intuitive pictures. One can however note that the 20th century brought some cases where one can predict, but cannot form a logical picture.

   That happened in quantum theory--the study of physics on the atomic scale, where space and time tend to be "grainy. " We can predict where an electron is likely to be observed, but cannot tell where it actually is.

   Physicists found such cases very unsettling, and some argued that an underlying reality of where the electron actually was remained a meaningful concept (some still do so). Einstein was among those, and said "I cannot believe that God is playing with dice. " Most physicists however (e.g. Richard Feynmann) believed that 'what we see is what we get' and that no "reality" existed beyond the probabilities which theory prescribes.

--Then go over section #9c in "Stargazers". Review the material, using the questions below:

Around 150 AD, a Greek scholar named Claudius Ptolemy collected all the results of ancient Greek astronomy in a series of books. His works were preserved by the Arabs, who combined them as the "Almagest. " It became a leading influence in European astronomy, especially after about the year 1200.

These planets are never seen far away from the Sun, but move back and forth from one side of the Sun to the other. The Greeks correctly imagined that they moved around the Sun and traveled with it around the celestial sphere.

The planets also traveled around the celestial sphere, following more or less the ecliptic, but now and then they would retrace their motion and move backwards for a while ("retrograde motion") before continuing forward.

Hipparchus and Ptolemy proposed that the outer planets followed "epicycles" around points that traveled around the celestial sphere and therefore, they thought, around the Earth. Their motion was like that of Venus and Mercury, except that for the inner planets, the center of rotation was visible, it was the Sun (or a point near the Sun), while the motion of the outer planets was not visible.

Hipparchus at first thought his theory predicted the motion, and believed that all such motions proceeded evenly around circles. As more accurate observations were made, all sorts of corrective motions had to be added.

"Copernicus" is the Latin version of Nicolaus Kopernik, (1473-1543). He was a Polish church official and an amateur astronomer, who proposed that the Earth was also a planet, and that all planets orbited the Sun in circles

Venus and Mercury were planets closer to the Sun, and therefore were only seen near the Sun, moving back and forth across it. Their orbital periods were shorter than the Earth's.

These planets had orbits were outside the Earth's, and they moved more slowly. The Earth's orbit, therefore, overtook them from time to time, and when it did, they appeared to be moving backwards in the sky.

Yes, but he was very cautious, because some important people opposed his ideas. He only published his work at the end of his life.

Galileo was an Italian scholar. His contributions were many, but he is mostly remembered as the first astronomer to build and use a telescope.

• The craters and "seas" of the Moon.

• The fact Venus changed shapes--crescent, etc.--like the Moon, confirming it was a sphere illuminated by sunlight.

• Four large Moons of Jupiter, forming a small "solar system" around that planet. This confirmed to Galileo the ideas of Copernicus.

• Sunspots, though others also observed them at about the same time.

• He discovered the rings of Saturn. However, Galileo's telescope was so crude that he was not sure what they were.

• The Milky Way, a whitish cloud stretching across the heaven: Galileo found it was composed of many faint stars. We now know that the Earth is part of the galaxy, a collection of about 100 billion stars, forming a flat wheel-shaped cloud. When we look at the Milky Way, we are seeing that cloud edge-on and therefore observe many distant stars.
  [Optional discussion: Should we say "the galaxy" or "a galaxy"? Actually, "the galaxy" was the term used for many centuries for this collection of stars--it means the milky way, from "gala," milk in Greek (and "galax" is a plant with milky sap!).

  Then in 1923 the American astronomer Edwin Hubble found evidence that the cloud-like "nebula" in the constellation of Andromeda was probably a distant galaxy like ours, an "island universe." In the years that followed Hubble found many other such "galaxies," together with evidence that the more distant ones were all moving away from us, suggesting an expanding universe. Nowadays, of course, the word "galaxy" is understood to be any such star-system ("Long, long ago, in a galaxy far far away... "); but it pays to remember that originally only one galaxy was known, namely ours.]

He aggressively promoted the Copernican theory, making enemies among powerful people, who claimed the Earth was the center of the universe and that all celestial objects revolved around it.

He had to proclaim that he was abandoning his Copernican views, and was forced to spend the rest of his life confined to a rural estate.

"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• About Tycho Brahe, his work and his connection with Kepler.

• About Kepler and his laws--and introduction to the subject.

• About conic sections, qualitatively.

• The mathematical formulation of the third law, and its explicit form for artificial Earth satellites.

• The student will confirm Kepler's 3rd law by comparing orbital periods and mean distances for all major planets.

Terms: Conic sections, ellipse, parabola, hyperbola, astronomical unit (AU).

Stories and extras: Story of Tycho and his supernova, some details about Kepler's life.

   Today we continue the story of the discovery of the solar system. Copernicus, as was seen last time, gave the first logical explanation of the motion of planets in the sky--not just formulas describing those strange motions, but an idea of what the solar system looked like.

   Old habits are hard to break. Copernicus had assumed all planets moved at constant velocities along circles, centered on the Sun, because after all, wasn't the circle the perfect curve, and the Sun the center of it all?

   Kepler tried to test this, and luckily, he could use some very precise observations, made by Tycho Brahe--the most precise astronomical observations before the invention of the telescope. Assuming that the planets moved in circles as Copernicus had proposed, Kepler calculated their expected positions. They did not agree, and the expected positions differed from the observed ones. Kepler had to conclude that the world was not as perfect as Copernicus had suggested. The planets speeded up and slowed down. Their orbits were not exact circles, and the Sun was not at the center of their orbits. Searching for a more accurate representation, he deduced what we now call Kepler's laws.

   About 70 years later Newton showed that all 3 of these laws were a consequence of the laws of motion and of gravitation, which Newton himself was the first to formulate.

That is how science makes progress:

   One, you don't guess what nature should be ("because it is perfect"), but observe what actually occurs.

   And two, you calculate. Kepler had a thorough command of the math needed to calculate planetary motion. Without that he could not have succeeded.

   The story of Kepler begins however with Tycho Brahe, an arrogant Danish nobleman who was also a talented astronomer. (Continue with the material given on the web.)

"

--Who was Tycho Brahe? and: What do you know about his nose? (Follow the link from the "Stargazers" section about him.)

Brahe was a Danish astronomer. He lost part of his nose in a duel and wore a false nose of gold-plated brass.

A bright "new star" appeared in the sky, never seen before. It was a nova, an erupting star. It was so bright it could be seen in the daytime.

Brahe made very precise measurements of the positions of stars.

Brahe used no telescope, none was known as yet. He used sharp eyes and a variety of graduated circles and of open sights, like the ones found on guns.

No, he did not agree with Copernicus. He recognized that the planets rotated around the Sun, but claimed the Sun rotated around Earth.

Kepler was an astronomer hired by Tycho to help analyze his observations.

Yes--Kepler believed the Sun was at the center of the solar system, that the planets revolved around the Sun and that the Earth, too, was such a planet.

About the shapes: Copernicus believed all planetary orbits were circles centered by the Sun.

About the motions:He believed that each planet moved along its orbit with constant speed. The greater the distance from the Sun, the slower was the motion.

He used the theory to calculate the positions in the sky where the planets were expected to be found.

Approximately yes, accurately, no. However, Ptolemy's theory did not predict them accurately, either.

Shape: that the orbits were ellipses--elongated circles [for the planets, very slightly elongated], and the Sun was at one focus--off center, shifted towards one end. That is Kepler's first law.

Motion: That the speed of a planet in its orbit depended on its distance from the Sun--the greater the distance from the Sun, the slower the motion. This relation could be expressed mathematically, and that expression was Kepler's second law.

If we cut a cone with a flat plane, an ellipse is one of the classes of cross-sections we may generate.

Yes, the circle is a special kind of ellipse. We get a circle if the cone is cut perpendicular to its axis.

Ellipses, parabolas, and hyperbolas.
[Demonstrate with a flashlight]

Cut the cone with a plane inclined less steeply than the straight lines which form the cone.

[Those lines, also called "generators", are like the poles which hold up an Native American lodge or "teepee. The "lodgepole pine" was particularly favored by the Indians for this use; it is a type of pine growing in the western US with straight thin trunks.]

Cut the cone with a plane parallel to the straight lines that form the cone.

[Orbits of non-periodic comets, the ones that appear unexpectedly, are often very close to parabolas; their sides become closer and closer to parallel as the distance gets larger. They come from the very edges of the solar system. Their orbits may really be very long ellipses, too close to parabolas to be told apart.

Periodic comets like Halley's, which moves in an elongated ellipse and returns every 75 years, presumably started that way, too, but were diverted by the pull of some planet, most likely by Jupiter, into elliptical orbits.]

Cut the cone with a plane inclined more steeply than the straight lines which form the cone.

[The sides of a hyperbola diverge at an angle: the graph y=12/x for instance is a hyperbola whose sides diverge at 90 degrees.

An object approaching the Sun in a hyperbolic orbit is probably coming from outside the solar system, and will never come back.]

He found a mathematical law, which connected the mean distance from the Sun and the time needed to complete one orbit. This was Kepler's third law.

The third law states that the square of the orbital period is proportional to the third power ("cube") of the average distance from the Sun.

Kepler's 3rd law states T² is proportional to a³. Call the factor of proportionality K. Then for two different planets, distinguished by subscripts 1 and 2, T₁² = K a₁³ and T₂² = Ka ₂³, with the same K. It follows that K= T₁²/a₁³ and also K = T₂²/a₂³. Setting the two expressions for K equal to each other, T₁²/a₁³ = T₂²/a₂³.

Yes, Kepler's laws apply to artificial satellites as well as planets.

It is still true. As Newton showed nearly 70 years later, any objects held in orbit by the gravity of a large central object follow Kepler's laws.

The pilgrims landed one year after Kepler announced his 3rd law, 11 years after his first laws.

"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• Learn or re-acquire the use of graphs in cartesian coordinates.

• Become acquainted with linear graphs, the parabola and the rectangular hyperbola. Also learn to prepare tables of paired values as preparation for plotting a line.

• Learn about graphs defined implicitly, without isolating y (or x). The circle is used as an example, also demonstrating a multiply-valued graph.

• Learn about the cartesian equation of an ellipse, with a worked example.

• Learn about the historical definition of the ellipse as the collection of points whose distances from 2 given points (the foci) has the same sum.

Stories and extras: The focusing property of an ellipsoid, in particular the focusing of whispers in the old chamber of the US House of Representatives. Also the painting of that chamber by Samuel Morse, inventor of the telegraph.

Start this lesson by explaining that the most useful and most common use of cartesian coordinates is to create graphs. On the board:

"A graph is a graphical representation of a mathematical relationship."

It is the bridge connecting shapes of lines, as seen by our eyes, with mathematical relationships and formulas.

Before getting into graphs (with which many of you here are already familiar, maybe all of you), let us first review what we know about Cartesian coordinates:

Start the discussion of graphs by a review of coordinates

-- What are "systems of coordinates"?

Methods of labeling points in space by a set of numbers, called their "coordinates."

The point's distances from two straight axes--the "x axis" usually drawn horizontally, and the "y axis" perpendicular to it

These are two numbers which give its position:

  x is the distance measured parallel to the x axis. It is measured from the y axis--to the right it is positive, to the left, negative.

  y is the distance measured parallel to the y axis. It is measured from the x axis--up is positive, down is negative.

They are (0,0), that is (zero,zero)

Yes

Polar coordinates also have an "origin" O as reference point, but instead of using (x,y) to label the position of a point P, they use the distance r from O to P, and the angle f ("phi"--Greek f) between the line OP ("radius"--hence the letter "r") and some reference line.

Graphs--the material of section (11a).

[Note to the teacher: It is easier for the student to start with concrete examples than with abstract formulas, which need mental translation]

  A graph is a way of using coordinates to present visually the relationship between quantities. The relationship can be something observed--for instance, stock market prices (for example, as given by the "Dow Jones Index") against time, or the temperature of a patient in a hospital against time, etc. When either of these graphed quantities goes up or down, the graph will instantly show it, also telling how steep and how big the change is.

  You should be familiar with graphs, they are widely used (if the students use graphing calculators, bring that up). Graphs are even more useful for mathematically defined variations, and can be used to represent many kinds of shapes--including ellipses.

Then present section (11a), using the questions below in the presentation and/or for review.

A line drawn in a system of coordinates, on which all points (x,y) satisfy some relation between x and y.

Yes; the relationship between x and y need not be a mathematical one. However, this graph will not include the origin, because we have no data before x = 1776.

A straight line.

[That is the example in the lesson. Draw the line on the blackboard, but don't label the axes, only the origin. Then as answers come in (below) label also the intersections with the axes with their values of y and x].

   For any value of x, plug it in to the right side, calculate the value of the expression and get the paired value of y.
  The collection of all such pairs describes a line, which turns out to be straight.

On the y-axis, x=0. Put this in the equation and get y=2.

On the x-axis, y=0, so    -(2/3)x + 2 = 0.
Add (2/3)x to both sides:    2 = (2/3)x
Divide by 2:             1 = (1/3)x
Multiply by 3:            x=3.

They are if the relation between x and y has the form y = ax + b, where a and b are two numbers of either sign.

They are not with other relations, e.g. y = 3x² which is a parabola, or y = 3/x which is a hyperbola [also, if you replace "3" by any other number, positive or negative]

You bet. It is a straight line parallel to the x axis and passing the y-axis at y=2. For any value of x, y equals 2.

  [One may add a comment on the word "linear" in mathematics. The equation of a graph giving straight line may also be written "ax + by = c", and mathematicians call this a "linear" expression.
  This has been generalized to more variables, for instance 3x + 5y -2z is said to be linear, even though the points in 3-dimensional (x,y,z) space which satisfy (say) 3x + 5y -2z = 11 do not form a line but a flat plane.]

A parabola. Describe on the blackboard.

[The example below is given for illustration. It should not be on any test, and is optional material].

A hyperbola. [Describe on the blackboard, tabulate and sketch]

x =	1	2	3	4	6	8	12
y =	12	6	4	3	2	1.5	1

and

x =	-1	-2	-3	-4	-6	-8	-12
y =	-12	-6	-4	-3	-2	-1.5	-1

Point out that at x = 0, y is not defined--it is + infinity if we approach from the right, - infinity if we come from the left, in either case the point cannot be drawn.

[The next question is best left for the teacher to answer]

--Does the equation of a line always have the form y = f(x) , where f(x) is "some expression involving x"?

[No. This form is however the one almost always used, because with it, finding points on the line is very easy. You just choose your value of x, plug it into the formula and immediately get the corresponding y.

   The "expression involving x" is called "a function of x" which is why the shorthand for it is f(x).

   However, any equation connecting x and y can be used. In such cases, if we choose x, we may need some extra work to get y.

[The next example shows one of them.]

Draw a circle on the board, mark its center with O, put a system of Cartesian axes through the center, select a point P on the circle, draw its radius R and its projection A on the x axis. Mark AP as y, OA as x.

x² + y² = 25

Because for any such point, the triangle OAP is a right-angle triangle, and the above relation follows from the theorem of Pythagoras.

On the x axis, y = 0, so x² = 25, giving two solutions, x=5 or x= -5

On the y axis, y = 0, so y² = 25, giving two solutions, y=5 or y= -5

It is the same circle as before--we only need to multiply both sides by 25 to show this is another form of the same equation as before.

It is an ellipse

[Optional: Where does it cut the axes?
Optional: Let us derive 2 additional points on the ellipse. (calculator needed--see text of the lesson). Students may do part or all of the derivation..]

Its greatest length and width.

16 and 8 units--not 8 and 4. Each half of the major axis is 8.

An ellipse is the collection of all points for which the sum of the distances R₁ + R₂ has a constant value

Foci--each one, a focus.

Because Kepler's first law places the Sun at a focus--not at the center of the ellipse, which is the origin of our axes.

[Tell story of old chamber of the House of Representatives in the US Capitol. First however ask the class if anyone had been to the capitol, and ask those who have, if they remember something special about the big room where statues were collected. Let a student tell it, later, if necessary, fill in more details.]

"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• Become familiar with graphs of the form r = F(f) in polar coordinates (r,f), in particular with the circle, ellipse and other conic sections.

• Will understand the role of the semimajor axis and eccentricity in determining the nature of an ellipse.

• Will understand that the fixed point in any planetary system is its center of gravity. (This is used in a later section in deriving the rocket principle).

Terms: Focus (of ellipse), eccentricity, semi-major axis, orbital elements, mean anomaly (qualitatively only), center of gravity.

Stories and extras: Method used in the search for other planetary systems, and the recently discovered planetsary system of Upsilon Andromeda.

(Suggested answers in parentheses, brackets for comments by the teacher or "optional")

   Start the lesson by reviewing polar coordinates. Then point out that in cartesian coordinates (preceding lesson) the ellipse is symmetric--around the axes and around their crossing point.

   The motion of a planet of a satellite in an elliptic orbit is not symmetric--the center of motion, the focus, is shifted towards one end, and the planet's distance from it goes up and down each orbit, like a wave.

    It suggests that cartesian coordinates are not the most suitable for handling orbits--and that, in fact, turns out to be the case. Polar coordinates, centered on the focus of the ellipse, are more suitable. As will be seen, the wave-like dependence of the distance is then clearly seen as a result of the wave-like variation of the cosine of the polar angle.

    Then present section 11b of "Stargazers," up to "Refining the First Law". Discuss the material, guided by the questions below, and conclude with "Refining the First Law" and its questions, as listed further below.

-- If a cartesian system (x,y) has the same origin as a polar system, and the reference line from which f is measured in the polar system is the x axis--given (r,f) of a point, what are its (x,y)?

x = r cos f          y = r sin f .

r² = x² + y².

[tan f = y/x]

[Note in this section we denoted the polar angle by f, not by f, because that is the notation used in the study of orbits. We will use capital F(f) for "a function of f" that is, "some expression involving f". ]

r = F(f) is one way.

[More generally, any expression F(r,f) involving (r,f)) can be used, for example in the form F(r,f) = a, where a is some number or zero. The important thing is that at least over some range, each f has some corresponding value of r--sometimes, more than one value.

For instance,the line

         3 r sin(f) - 2 r cos(f) = 10

What sort of line is it? Don't panic! It is just a straight line, as you easily see once you convert it to cartesian coordinates, using the relations developed earlier for the (r,f) notation.

A constant number R, equal to the radius. Then r = R for any value of f.

[This is similar to the straight line y = 3. On that line, the value of y is the same for any x, and therefore the value of x does not have to appear.]

A number between 0 and 1, known as the eccentricity of the ellipse.

Smallest for f=0, cos f =1; biggest for f=180°, cos f = -1.

         r = a(e-1)(e+1)/(1 + e cos f)

[The class should know this identity, or else, it may be proven on the board.]
Using that form, what are the biggest and smallest value of r?

A student or the teacher derive these on the board: biggest a(1+e), smallest a(1-e).

[Optional: Draw on the board an ellipse, around its focus, and on it, show the biggest and smallest r.
    If this is the elliptic orbit of an Earth satellite, the smallest and biggest distances are know as perigee and apogee, where "gee" stands for "geo", the Earth.
   For planets orbiting the Sun, these are called the perihelion and aphelion, from "helios", the Sun.]

It is the sum of the smallest and biggest distances: a(1+e) + a(1-e) = 2a.

They are quantities used to define an orbit.

The semi-major axis a and the eccentricity e

a is the radius, e is zero.

The semi-major axis a is the precise meaning of the "mean distance" we used earlier. The square of the orbital period T is proportional to the third power (cube) of the semi-major axis.

Six elements exist: a and e define the orbital ellipse, the mean anomaly M is an angle that defines the satellite's position along that ellipse and 3 additional angles define the orientation of the orbital ellipse in 3-dimensional space.

[We can extend the equation of an ellipse to e = 1 or even e > 1, but must be careful. Suppose we draw a series of ellipses, of increasing e, all with the same minimum distance a(1-e). Then as e approaches 1, the semimajor axist grows to be larger and larger.

   With e=1, we have something infinite (a) multiplying something that is zero (1-e). We thus need to rewrite the equation in the form r = p/(1 + e cosf) With e = 1 this gives a parabola, with e>1, a hyperbola.]

Neither--each rotates around its commen center of gravity.

Planets are too dim and too close to their suns to be seen by today's telescopes. However, each such sun also moves, around the joint center of gravity of it and of its planets. For instance, with just one planet, the Sun is always on the opposite side of the center of gravity.
Therefore, if astronomers see a slight wobble in the position of a distant star, they may deduce from it the existence and motion of its planets.

"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• Get an intuitive understanding for the way orbital velocities vary along each orbit, according to Kepler's second law.

• Get a first exposure to the concepts of "potential energy" and "kinetic energy." Motion in the presence of of gravity, in everyday life, conserves total energy, but can swap one form for another--as in a roller coaster, which speeds up at the low points and slows down at high ones.

• Know that orbital motion conserves also energy, in a somewhat similar way, although the formulas look different.

• (Optional) Learn (very qualitatively--how orbital motion is calculated: the polar angle f, ("true anomaly") varies unevenly around the orbit, but another angle, the "mean anomaly" M, varies steadily, and formulas exist to derive from M yet another angle, the "eccentric anomaly" E, from which f can be obtained by another transformation.

Note: At this stage, knowing that M exists is the most the student can do. An optional section (12a) "How Orbits are Calculated" goes further into the subject, but is not covered in these lesson plans. It introduces the student to the idea of successive approximationa for solving a difficult equation--here, "Kepler's Equation" which relates M and E. It also describes what the other orbital elements are.

Terms: Perigee, apogee, perihelion, aphelion, radius vector; Energy, kinetic energy, potential energy, conservation of energy, escape velocity, [true anomaly, mean anomaly, eccentric anomaly]

Stories and extras: Thomas Jefferson's clock in Monticello, driven by suspended cannonballs.

With suggested answers, brackets for comments by the teacher or "optional")

[Note to the teacher: Enrico Fermi, the Italian physicist--Nobel prize winner, one of the founders of nuclear physics and designer of the first nuclear reactor--once described the way he felt a lesson should be given:
"Tell them what you are going to tell them, tell them, then tell them what you told them."
What follows below follows the first part of Fermi's advice.]

   As we will see, the meaning of Kepler's 2nd law is "planets speed up when closer to the Sun, slow down when further away."

   We already know another motion which does exactly that: a roller coaster speeds up in the "valleys," slows down on the "hilltops." The two motions are related: both involve gravity.

   As we will see, both also involve something known as energy. That energy comes in two forms--energy of speed, or kinetic energy, and energy of position, or potential energy, higher at the hilltops and higher at apogee. The sum of the two is kept constant--which is why, as the roller-coaster carriages rush down the steep slope or the satellite approaches Earth, both gain speed, losing it again as they pull away.

Let us go into the details.

(Here give the material of section (12), except for the optional part about the true and mean anomaly, which (if included) is given separately.

The questions below can be used in the lesson and/or in the review afterwards.

The line between it and the Sun. [strictly speaking, center-to-center]

The closer the planet to the Sun, the faster it moves.

Yes, it does.

[What follows next is a calculation: you may let one of the better students "help you with it" at the board, illustrating the problem with a drawing as you describe it. The rest of the class should copy.]

Here is how. Let us mark the distances the satellite covers in one second-- D₁ at perigee, D₂ at apogee (enter in drawing). The area covered in one second by the radius vector at perigee is a triangle, its base is D₁ and its height is r₁, and the two lines are perpendicular. Its area is therefore...?         (1/2) r₁ D₁

A similar triangle at apogee (draw) has area ...?

                      (1/2) r₂D₂     (shades of "Star Wars"!)

Therefore...? By the second law, r₁ D₁ = r₂D₂. But the velocity is defined as the distance covered in one second, so in place of (D₁,D₂) we may just as well write (v₁,v₂), the velocities at both these points. So...

r₁v₁ = r₂v₂

Divide both sides by r₁v₂ to get

v₁/v₂ = r₂/r₁ .

The second ratio is 10, so the first ratio must be 10 too: the velocity near Earth is 10 times larger.

No. At other points, distances such as r₁ and D₁ are not perpendicular to each other, and the area of the triangle also depends on the angle between them.

The stone slows down as it rises and loses energy, then regains velocity and energy as it falls down again.

Loosely, anything that can make a machine move.

Have the students answer: electricity, calories in food, heat, sunlight, sound, nuclear energy...

The total energy in an isolated body or system of bodies is conserved, though it can change from one kind to another.

[This part is best handled by the teacher without much elaboration. Energy will come up again in section 15 and will be discussed there in a more complete fashion. Here students are told what the energy of a moving satellite is, but remembering the formula may be optional].

Kinetic energy and potential energy.

Energy of motion.

The amount of matter being moved (the mass m) and its velocity v. The formula is E_K = (1/2)mv².

Energy due to position.

m g h, with g close to 10, the acceleration due to gravity.

E = (1/2)mv² + m g h = constant.

As one part grows, the other decreases to keep the sum the same.

At the bottom of its swing, its speed is largest, and therefore, so is its kinetic energy. At the top of its swing, it comes to a brief stop: its kinetic energy is zero, but its height and therefore its potential energy are largest. It therefore seems reasonable that the sum of the two energies stays the same.

...exactly the same as the swing.

The constant which gives the value of E will depend on it, but we may use any reference height we wish.

[Note: the energy equation of an orbiting body may be too much to memorize, so in the question below, the student is given the formula and is only asked to explain its meaning.]

E = 1/2 mv2 - k m/r = constant

  Where k = gR_E². It has a different expression for the potential energy.   With a stone, the higher we lift it, the greater is its potential energy: is this also true here?

  (Yes, though the fact the potential energy is negative may be confusing. The higher the satellite goes, the larger r and the less negative the potential energy is, which means it grows: at infinity it is zero, a number larger than any negative value.

  This again illustrates that the value of the potential energy E_P depends on the reference level at which we choose E_P = 0. Any reference level is OK: what matters are differences in potential energy, which dictate the gain or loss of kinetic energy E_K.

The velocity with which an object would fly off the surface of the Earth and never return.
    (Note however, we are talking about motion relative to the Earth alone. In practice, such an object would still be in orbit around the Sun. To also escape the Sun's gravity would take considerably more energy!)

[Give details on the blackboard as you go along, and let students copy.]

The energy of an object with velocity V, at the surface of the Earth, is

        E = 1/2 mV² - k m/R_E

When the object is far enough from Earth to be considered "escaped", its distance r is so big that its potential energy k m/r is virtually zero. Also, it has used up all its kinetic energy to get so far, hence v=0   too.

This suggests that for such a motion E=0. Then

        1/2 mV² - k m/R_E = 0
so
        V² = 2k/R_E = 2gR_E     (k=gR_E²)

If we calculate in meters and seconds, take g = 10, RE = 6 371 315 meters... quick, the calculator!

The polar angle f in its orbiting motion, measured from the position of perigee (or perihelion).

One calculates the mean anomaly M, an angle which is also zero at perigee, but which grows at a constant rate--unlike f.

Transformations exist from M to an intermediate angle E ("Eccentric anomaly") and from E to f.

[For students familiar with trigonometry, or those who have gone over sect. 11a]

We can obtain its position in the orbital plane, because we then can calculate r = a(1 - e2)/(1 + e cos f), giving its location in polar coordinates.

But we still need to know how the orbital plane is oriented in 3-D space, which requires 3 more inputs:

   (1) the inclination of that plane to the equator

   (2) in which direction on that plane does apogee point.

   (3) The orbital plane can still be rotated around the Earth's axis without changing its inclination. Imagine a slanted board on a record turn-table; one more angle is needed to give the amount of rotation of that turntable.

An introduction to the concept of acceleration and to motion under the influence of gravity, starting with free fall and ending with motions that start out with both horizontal and vertical initial velocities.

"From Stargazers to Starships" home page and index:
          http://www.phy6.org/stargaze/Sintro.htm

• Light and heavy objects fall at the same rate, as established experimentally by Galileo.

• Falling objects, and balls rolling down an incline, tend to accelerate at a constant rate a. Their velocity increases as v = at.

• The acceleration of free fall is g = 9.81 m/s².

• With initial velocity u, v = u + at. Use this to calculate height attained by object thrown straight up.

• Distance covered is S = a(v_initial + v_final)/2 = ut + gt²/2

• Fallacy of the "road runner paradox": when two different motions involve an object they act simultaneously--never consecutively. E.g. in shooting at a distant target, the gunsight make us aim at a higher point, so that the fall of the bullet brings it to the target.

• Possible addition by the teacher: artillery.

Terms: Acceleration, velocity (also initial, final and mean velocity), speed (=magnitude of velocity), "g" the acceleration due to gravity.

Stories and extras: Legend of Galileo dropping balls from Tower of Pisa (also of his timing the swing of a chandelier). "Road runner" cartoon, demonstration of feather falling on the airless Moon.

Hands on: Possibly, Galileo's experiment with the inclined plane

Starting out:

Use Galileo as starting point.

We remember Galileo for several things:

1. He was the first to observe the heavens through a telescope (which he had designed and built)
2. He was persecuted for advocating the Earth went around the Sun.
               But he also:
3. Was a pioneer of physics, introducing the idea of experiments--rather than try guess what nature might be doing, using logical arguments, observe what it does do.

  The legend is that as a boy, sitting in church with his family, Galileo became bored and to pass the time, he observed a swaying chandelier. Using his own pulse to time the swings, he discovered that they always took the same length of time, whether they were big or small.
  The story may well be a legend--but Galileo did make such observations, and they led to a better design of clocks.

  He certainly studied the fall of objects. Philosophers had argued that a heavy object fell faster. According to another legend, he climbed the leaning tower in the town of Pisa--a bell tower whose foundation settled soon after it was built, causing it to lean--and from the top dropped heavy and light balls. A helper on the ground observed that they arrived together.

  Galileo learned to be careful in his experiments. It was known that thunder arrived some time after the lightning was seen.Firing a gun and timing the interval between the flash and the sound allowed the speed of sound to be measured. But did light travel instantly?

(Teacher may ask class--how would you find out?).

  Galileo posted himself and a helper at night, a good distance apart, each with a lantern covered with a screen. Earlier, the helper was told--when you see the light, lift your screen. Galileo then lifted the screen and looked how long was the delay until he saw the return flash. The light, during that time, had to travel back and forth between him and his helper.

(Teacher may ask class--do you see any problem with this experiment?)

  There was a delay, but Galileo realized it might just be the reaction time of the helper. He therefore repeated the experiment with the helper at a much greater distance. The delay was the same--and Galileo concluded that the velocity of light was too big to be measured this way.

  Now back to falling objects. Galileo showed light and heavy ones fell together: he did not ask why; that question was later taken up by Newton.

  [Sometimes people argue the reason is clear--take the big stone, divide it into 10 little stones. When those stones were together they fell the way the big stone fell, so when they are apart, shouldn't they fall at the same speed? Answer: in air, yes, in water, no.]

The thing we note about falling objects is their velocity: it starts slow and gets faster and faster.
  What is velocity, anyway?... Then go on to acceleration.

---

Guiding questions and additional tidbits

---

-- What is the velocity of a moving object?
The rate at which it covers distance.

---

-- What is speed?
The magnitude of the velocity. We may use the terms interchangably now, but in a later stage we will also have to pay attention to the direction of the velocity.
[Using "velocity" at this stage justifies the use of "v" and also of using "+" or "-" signs.]

---

-- If an object covers distance S meters in time t seconds--what is its velocity [or speed] v?
v = S/t meters per second, abbreviated m/s. (Strictly speaking, that is its average velocity.)

---

-- If an object covers distance S miles in time of t hours, what is its velocity?
v = S/t miles per hour or mph (again, average velocity).

---

-- A biker pedals at 10 mph. What is the biker's speed in meters/sec?
1 mile=1609 meters.

16090 meters in 3600 seconds, S/t = 4.47 m/s

---

--What do you know about the speed of a freely falling object?

It constantly increases, at a steady rate.

---

-- What is the acceleration of an object?
The rate at which its speed grows.

---

-- Can acceleration be negative?
Yes. You jump from a table: the moment you leave it your speed increases and your acceleration is positive. When you hit the ground, your acceleration is negative.

[More generally, acceleration like velocity can have any direction, but for now we do not go that far.]

---

-- What can you say about the acceleration of a freely falling object?
It is constant, equal to about g = 9.81 m/sec².

---

-- How fast does a falling object move after t seconds?
v = gt = 9.81 t m/s

---

-- How much is that in miles per hour?

First, the conversion factor needs to be derived. Using a previous answer,

10 mph = 4.47 m/s     Divide both sides by 4.47
        10/4,47 = 2.237 mph = 1 m/s.
So v = (9.81* 2.237) t mph = 21.95 t mph.
        After 3 seconds, more than 60 mph!

---

-- How is this modified if we throw the object downwards, and start it not from rest but with an initial velocity u?
Then u is positive, and adding it to the fall velocity gives v = u + gt

---

-- What if we throw it upwards?
Then u is negative. If we want to only use positive quantities, define the positive speed u' = -u, so v = -u' + gt . As long as v is negative, it moves up, positive, it moves down.

---

-- After how long does it reach greatest height?
At greatest height, v = 0, u' = gt, t = u'/g.

---

--How do we calculate the distance covered?
We multiply time t by the mean velocity.

---

-- What do we take as mean velocity?
Half the sum of initial and final velocities.

[Note that we have only guessed that with this definition, v_mean*t=S. We have not proved it. Actually, this only works if the acceleration is constant. If the acceleration changes as time goes on, using this mean velocity in v_mean*t usually does not give the right S. ]

---

--What then is the distance S?
S = 1/2[u + (u +gt)]*t = ut + (1/2)gt²

---

-- We throw a stone upwards with velocity u'. How high does it get?
From the previous example, u = -u', and the time t needed for reaching the greatest height is u'/g. So:

    S = ut + (1/2)gt² = -u'(u'/g) + (1/2)g(u'/g)2 = -(1/2)(u')²/g.

The minus sign means, it is in the direction we chose as negative, above the starting point.

---

-- What is the distance with constant acceleration a?
S = 1/2[u + (u +at)]*t = ut + (1/2)at²

---

-- If a ball rolls down an inclined slope, because of its weight, does it accelerate?

Yes. If we neglect friction, the acceleration a is constant.

---

-- How did Galileo confirm the constant acceleration of a ball rolling down a slope?
The answer is in the "Stargazers" section.

---

-- When we throw a stone horizontally with a velocity w, how does it move?
Neglecting air resistance, it simultaneously moves horizontally with a velocity w while falling vertically with acceleration g.

If we plot the motion in (x,y), with x growing horizontally and y growing downwards, then
x = wt y = (1/2)gt²

---

-- When "Road Runner" runs over the edge of a cliff, how does he move?
The same way.

---

-- When we fire a rifle towards a target at a rifle range, how does the bullet move?
The same way.

---

-- When we fire a rifle towards a target in a rifle range, what do we do to score a bull's-eye?
We aim towards a higher point, so that the fall of the bullet brings it to the level of the bull's eye. The gunsight can be adjusted to raise the aim by an amount appropriate to the distance of the target.

---

-- When shooting arrows using a bow, how do we aim for the target?
Same way--aim higher. Here the shift is greater, because arrows travel more slowly. With a given distance, they have a longer time to fall and therefore drop a longer way down.

---

Optional: Artillery. A cannon gives the shell both an upward velocity u' and a horizontal one w. Three kinds of cannon exist:
(1) High speed cannon, like those on tanks. They fire near-horizontally, like rifles, and are aimed at the target--with correction for the drop of the shell. Problem--to get the high speed takes a heavy, expensive cannon, with a strong recoil that somehow has to be absorbed.

(2) Howitzers, which are aimed around 45 degrees up, at which angle they get the greatest range. For the same range, therefore, they need less velocity, and one can use a lighter cannon. But to aim it, a forward observer is needed--presumably, linked by radio, telling the gun crew how to correct its aim.

(3) Mortars, firing at a steep angle, e.g. 60 degrees. That way the ground absorbs the recoil, allowing a light, portable gun (the smaller kinds can even be carried by hand), still firing a fairly heavy shell. However, it will not shoot very far--nor will it be very accurate, because the slow shell with a high path spends a long time in the air and is easily deflected by wind.

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:         ....stargaze/Lintro.htm

Note: This lesson uses vectors, and some way of denoting them on the board and in the notebook must be agreed on by the class. In this lesson plan, all vector quantities will be underlined.

• About the definition and purpose of vectors, in mathematics and physics.

• To use vector addition for representing the sum of two motions taking place simultaneously.

• To resolve vectors into components along the directions of given axes, in two or three dimensions.

• To add two or more vectors, using components

• To resolve forces on an object that rests on an inclined plane.

  Terms: Vector, vector addition, vector components, magnitude of a vector, vector components parallel and perpendicular to a given direction.

  Stories and extras: None here; however section #22a on airplane flight has some interesting applications, which could follow this lesson.

  Starting out:

  Today we discuss vectors, mathematical object which have not only a magnitude, a size, the way ordinary numbers have, but also a direction in which they point. They can be approached in different ways.

  1. They can be viewed as a wider definition of numbers. Numbers can be defined in stages, each stage generalizing the previous one but covering a wider class, like circles within circles. (Illustrate on the board by a line on which numbers are marked, also write underlined terms in a table--each new one below the preceding ones.).

       The earliest numbers were integers: 1,2,3,4 .... and so on, invented very early, for practical purposes--say, counting sheep as they came home, to make sure none is missing.

       Then negative numbers: -1, -2, -3... --you owe me one, two, three sheep. Also zero, which was only regarded as a number fairly late.

       Then fractions--1/2, 1/3, also 7/12 or 3/7 and so on; the Egyptians only knew the first kind, and would write the 3rd and 4th fractions as (1/2)+(1/12) and as (1/3)+(1/12)+(1/84). Also decimal fractions.

       Then "irrational numbers" such as the square root of 2 which cannot be written as any fraction (there is a simple proof). What next? All these together are known as real numbers, to distinguish them from (complex numbers) which inlude i, the square root of (-1), and expressions such as a + bi, where a and b are real numbers. This however represents a direction in which we will not go today (which is why the term was written in parentheses). It may be noted in passing, however, that complex numbers have a close connection to vectors in 2 dimensions.

       So instead, what will it be? All the above can be related to points along a line: integers are isolated points, fractions seem to fill the spaces between them quite densely, but they still leave enough space to squeeze in the irrationals.

       Now, presumably, all the points on the line are covered. For each number we can put an arrow on the line, the distance from zero to that number--arrows to the right (say) for positive numbers, to the left for negative ones.

       Vectors are mathematical objects that represent arrows in any direction--in the plane, even in 3 dimensions. It is a new level of "numbers", and that is one way of looking at them.

       In algebra, we mark ordinary numbers ("scalars") with letters. If we want to show a quantity is a vector, mark it with an arrow above, or an underline or (mainly in books) in bold face. In the web files of "Stargazers," unfortunately, bold face is used to highlight quantities, so this convention is not followed, and you will have to distinguish vectors from their context.

  2. Mathematicians have invented all sort of strange generalizations of numbers. The ones of most interest are the ones with good applications.

  Similarly, forces, accelerations, magnetc fields from several sources, all are added like vectors. Engineers who put up a bridge or a building and want to make sure all forces balance, etc., need vectors.

Enough talking about them--any examples?
  The simplest kind is displacement (sketch on the board a map of the US and use it). You take a pencil and displace it from New York to Chicago, then from Chicago to Seattle. The final effect is the same as if we displaced the pencil from New York to Seattle.

  The displacement from New York to Chicago is this arrow.
  From Chicago to Seattle -- this arrow
  From New York to Seattle --this arrow, and we say it is the vector sum of the other two arrows.

  It may look like a strange way of adding--but that is also how you add velocities, and forces, and magnetic fields.

(now to the lesson)

--What is the graphical method of adding two vectors?

Place the tail of the second at the head of the first--the sum is from the tail of the first to the head of the second

No.

The two additions always forms a parallelogram, because each arrow appears twice, and the directions must be parallel.
The sum then is the diagonal of the parallelogram.

        When they all are along the same line.
--But vectors along a line can have two directions!
        That is right--vectors in one direction are counted +, in the other -

The questions below are just quickies: the teacher can add more serious ones.

5 mph, 15 mph.

Because the tread is moving in the opposite direction at 5 mph. The total velocity is therefore zero.

V² = 12² + 5² = 14400 + 2500 = 16900.     V = 130 mph.

To represent it as the sum of two other vectors--usually, in prescribed directions.

Because the directions of the air speed and wind speed may have odd angles.
    Rather than deal with those angles, it is easier to resolve each into a north-south and an east-west component, add up the components in each direction (like numbers) and then form the sum again.

Due north at 79.32 mph. Let V be the airplane's velocity, W the wind's velocity, and let us resolve these vectors in an (x,y) system with the x-axis pointing due east and the y axis due north. The components are:

V_x=-120 sin 17.13°= -35.36     V_y=120 cos 17.32° = 114.68
W_x= 50 cos 45° = 35.36         W_y= -50 sin 45°= - 35.36

The x-components cancel, the total y-component is
114.68-35.36 = 79.32

--Let us turn the customary (x,y) axes clockwise by 90°, so that down is the x direction, and perpendicular to it, to the right, is the y direction.

(Draw on the board). That means, downward x velocities are positive and an initial x-velocity u is negative if directed upwards.

Also the initial horizontal velocity w is positive when directed to the right

We can calculate the velocity of each motion:

V_x = u + gt               V_y = w

Together they give the velocity vector V. The displacement vector S similarly has components:

S_x = ut + (1/2)gt²                S_y = wt

We note (u,v) are the (vertical, horizontal) components of the initial velocity, which we can call V₀. So (firing in the y direction, say)

         u = -1000*sin 45° = - 707 m/s
         w = 1000*cos 45° =   707 m/s

At impact, S_x = 0, so          ut + (1/2)gt² = 0

One solution is t=0--it holds no interest, just tells us we started from ground level. Divide by t (it is not zero, so we may divide by it)

-u = (1/2)gt          t = -2u/g = 141.4 sec
S_y = 99.97 km, approximately 100 km.

Air resistance may cut it down to less than half.

They have to overcome the component of the weight parallel to the surface of the ramp, which is 1000*sin 5° = 87.15 kg.

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:             ....stargaze/Lintro.htm

• The concept of energy, using a variety of examples and also the analogy between energy and money.

• The conservation of energy in its conversion from one form to another.

• Units of energy--Joule, calorie, also watt and kilowatt-hour.

• The special nature of heat, as the "soft currency" of the energy world.

Terms: Energy (potential, kinetic, conservation of), pendulum, joule, calorie, second law of thermodynamics. (kilojoule, kilocalories)

Stories and extras: The energy content of a candy bar.

Today we will study energy,so we might just as well start by asking--"What is energy?"

Solicit answers; stop if someone says "what it takes to run a machine."

If someone gives the formal definition "ability to do work" ask:
"What then is work?" If the answer is "force times distance" say, that is correct; however, that definition will have to wait until the class has learned what a force is.

We could redefine it as "overcoming resistance over a distance"--for instance, lifting a brick (against gravity) from the floor to the table, or dragging it along the floor (against friction), and then work equals resistance times distance.

Any of these could also be done by a machine, so for a start we will simply say "energy is anything that can run a machine."

--Electricity, if you used electric lights, or a radio, or TV
--Light--that was what the electricity in the lightbulb was converted to
--Sound--that was what the electricity in the radio was converted to
--Chemical energy--when you ate breakfast, it gave you strength.
--Heat--if you cooked your food, or heated the house.
--Nuclear energy--if you enjoyed sunlight, because the Sun gets its energy by combining atomic nuclei of hydrogen to helium, deep inside it.

That energy becomes heat, and heat causes light to come out.
In an electric lightbulb, electricity makes a wire very hot, and that heat is what produces light.

On a bike, the chemical energy of your food is turned to motion, through your muscles. You can build up speed--that is kinetic energy--or you can climb up a hill--that is potential energy.

And you know you can trade one kind against the other: rolling down a hill, you lose height as you gain speed, and that speed helps you get up the next hill (the same in a roller coaster).

gh = v²/2

In the absence of friction, the final speed v is the same no matter how the object came down--sliding down a smooth inclined ramp, or even a roller-coaster track, still gives the same final speed.

[The teacher may note that while the final speed is the same, the time taken to reach bottom isn't.
  For example: sliding down an inclined board like the one used by Galileo, the object gains speed much more slowly, yet the distance it must cover is longer, so that the time required is much longer, too.]

Yes, the sum (gh +v²/2)

You expect a bigger moving body to have more energy--a rolling bowling ball more than a rolling marble. For that reason we must multiply by mass m:

E = mgh + (1/2)mv²

We have not yet defined mass; for the time it is understood to be "the amount of matter in motion," which we can measure by weighing.
Later we will find a way of measuring mass that does not involve gravity.

A note about units. In any calculation in physics, we must always pay close attention to the units we use. If inappropriate units are used, mistakes easily creep in, fulfilling "Murphy's law"--if anything can go wrong, it will.

In all our calculations involving Newtonian mechanics (unless explicitely stated otherwise) the so-called MKS units are used--distances in Meters, masses in Kilograms, time in Seconds, and all derived units based on these three. In those units g = 9.81 and energy comes out in joules. Whenever other units are given, be sure to convert them to MKS!

Work is overcoming resistance over a distance--multiplying the resistance by distance. A mass m (see next lesson) has weight mg, and lifting it a distance h performs work

W = mgh

Joules.

h = 9*0.305 = 2.745 meters, m = 150*0.454 = 68.1 kg. If g = 9.81 m/s², then

W = mgh = 1833.8 joule

Into the potential energy of height.

From the chemical energy of the food you ate. But note (below) that you do not "burn many calories" by climbing one floor, compared to the number you get from food.

  Suppose you have eaten one square of chocolate weighing 4 grams (1/8 of a bar weighing one ounce). The chocolate contains 2 grams cocoa fat, providing 9 calories per gram (typical for fats), and 2 grams sugar, a carbohydrate with 4 calories per gram, for a total of 18 + 8 = 26 calories. These are "kilocalories" of 4180 joule each, so that piece of chocolate has given you the equivalent of 108,680 joules. If your body can convert it to muscle power with an efficiency of 10% = 0.1, you get 10,868 joules of usable work from that piece of candy, enough to climb 10,868/1833.8 or about 6 floors.

Your potential energy of 1833.8 joule is converted to kinetic energy of (1/2)mv² = 34.05 v² . Then v² = 53.856 , v = 7.3387 m/s.

In miles-per hour (1 mile = 1609 meters).

v = 7.3387*3600 = 26,419 meters/hour = 16.4 miles/hour.

Food energy creates body warmth, also powers the many chemical reactions required by life. In addition, the air we breathe out contains moisture (breathe onto a cool mirror to see it!). Energy is needed to convert the water we drink to vapor.

On the table of energy conversions, which form is converted into which:

-- In an electric fan?

Electric to kinetic

Electric to potential.

In principle, yes, the motor can become a generator when turned from the outside. In practice, it is too complicated to return power to the public supply. But we can absorb electric power generated this way, turning it to heat in a resistor, and that way brake the motor.

Electricity to light.

In a diode, electricity is directly converted to light. In a lightbulb, it creates heat, and the heat creates light.

Chemical to electric.

Yes, when the battery is charged.

Heat to kinetic energy. We will later see that the converging-diverging design of the nozzle is very efficient in it.
Has anyone here read or seen "October Sky"? It is a true story of high school boys building and flying rockets, and after they discovered the proper design of the nozzle, their rockets flew much higher.

Limestone is heated over fire in a kiln. It is a compound of calcium, oxygen and carbon dioxide. The heat drives off the carbon dioxide and crumbles the stone to calcium oxide, quicklime, which holds more chemical energy.

For use in mortar, builders slake the quicklime with water. It heats up, returning its chemical energy to heat.

Spacecraft near Earth use solar cells, that convert light to electricity--sort of the inverse effect of a light-emitting diode.

Around the outer planets, sunlight is too dim to provide enough energy in this way. Spacecraft that fly there, e.g. Voyagers 1-2 and Pioneers 10-11, use radioactive sources which generate heat, and thermocouples convert it to electricity.

The Russians experimented with small nuclear reactors on spacecraft. One crashed into a lake in Canada, contaminating it with radioactivity and creating great resentment; no such reactors are flown any more.

Power is the rate at which energy is supplied, measured in watts. One watt is 1 joule/second, 1 kilowatt = 1000 watt.

Energy: 1 kwh = 3,600,000 joule.

Because we usually cannot convert any of it back to other forms.

That one can never convert heat completely back into other forms of energy, some of it is always irrecoverable.

[Optional: The fraction of heat energy which can be converted to other forms depends on the temperature at which the heat is provided.
The unrecovered heat is changed to a lower temperature, and the fraction we recover depends on these two temperatures--the one at which the heat is received, and the one at which the remainder can be dumped.
A power station needs not only a supply of hot steam, but also a way of dumping the heat left at the end of the cycle. Steam locomotives dumped their spent steam into the air, and therefore needed a great amount of of water, carried in their tenders. Electric power stations (of any kind) recycle their steam and cool it with air in cooling towers, like those of 3-mile island which (for some reason) became a symbol of nuclear energy. Other power stations use nearby lakes and rivers to cool and condense their steam, and. steamships (of course!) do so with seawater.]

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:             ....stargaze/Lintro.htm

Note: This lesson uses vectors, and some way of denoting them on the board and in the notebook must be agreed on by the class. In this lesson plan, all vector quantities will be underlined.

• About Isaac Newton and his work.

• About Newton's laws of motion.

• The meaning of the first and third laws.

Terms: Force, mass

Stories and extras: Why a bicycle cannot be balanced unless it moves and why a boat slides back when one jumps from it.

  In the 1600s, the picture of our world seemed to come together. The world had a regularity and certain laws: Copernicus made sense of the motion of the Earth and planets, Kepler made it possible to predict such motions, Galileo found a regularity in the falling of objects.

But that seemed just a beginning. Every observation, every solved problem, seemed to bring up new questions:

• When a cannon was fired, it recoiled back: why?
  
• A swinging pendulum had almost exactly the same period whether its swing was wide or narrow: why?
  
• Why did planets move according to Kepler's laws? Was there something universal behind this regularity, so that anything orbiting the Sun or a planet followed those laws?
  
• Why didn't big stones fall any faster than small ones, if the force pulling them down was so much larger?

Newton, born in 1642, guessed that there existed some basic laws which governed these and other motions. If we understood those laws, we could explain everything. He was right, and he discovered those laws, too--they are now known as Newton's three laws of motion.

It is easy enough to state them, to learn what they say, but that is not enough. To use them properly, one must understand their meaning and become familiar with them through examples. Today we begin the process, and we will proceed quite carefully.

(Suggested answers, brackets for comments by the teacher or "optional")

He was perhaps the greatest scientist Britain ever produced, and his contributions included:
1. the laws of motion
   
2. the "theory of universal gravitation" and
   
3. the theory of quantities which vary and change continuously ("differential and integral calculus," co-discovery with Leibnitz in Germany)

[He also: built the first telescope based on concave mirrors, discovered "Newton's rings" which were a clue to the wave nature of light, proved the "binomial theorem", introduced "Newton's approximation" in solving equations, studied the flow of heat, and much more.]

[Possible project: have a student prepare 5-minutes presentations on Newton, based on web sites, encyclopaedia entries and other material.]

(1) Force, which was the cause of motion

(2) Mass, the amount of matter, which resisted motion.

  True, weight also increased with mass: a big stone was pulled down with a greater force than a small one. But it fell no faster, because it also resisted motion more than a small stone.

Motion with a constant velocity did not require any forces. Without anything opposing it (friction with the ground, air resistance), once such motion began, it could in principle continue indefinitely.

Acceleration required a force.

[All this is the modern formulation of Newton's laws. Newton himself based his laws on the concept of momentum p = mv , which requires the use of calculus: F = dp/dt. However, here we try to avoid calculus.]

The acceleration was

(1) In the direction of the force
(2) Proportional to the force
(3) Inversely proportional to the mass being accelerated.

Newton's second law.

a = k F/m with a and F vectors, and k some constant number expressing proportionality.

We can choose k=1 and that way define the units of F: the law then becomes a=F/m or F = ma.

[The teacher might also raise the question "how can you divide a vector by m"? Answer: you are not dividing by m but multiplying by 1/m. What it all amounts to is, dividing the magnitude by m.]

In the absence of forces, an object ("body") at rest will stay at rest, and a body moving at a constant velocity in a straight line continues doing so indefinitely.

No. The Earth moves in an elliptic orbit, not in a straight line, and its motion is subject to forces, mainly the Sun's gravity.

Forces are always produced in pairs, with opposite directions and equal magnitudes. If body #1 acts with a force F on body #2, then body #2 acts on body #1 with a force of equal strength and opposite direction.

Yes.

What was wrong with their argument?

Rockets push themselves forward by pushing their exhaust gases in the opposite direction. Air is not needed.

No, doing so will only cause it to lean more, by the third law. You control the lean by turning the handlebars, which shifts rotational momentum; the details are not explained here.

The recoil from pushing out the water.

"Mass Aboard Skylab" section #17a
          http://www.phy6.org/stargaze/Sskylab.htm

"Comparing Mass Without Gravity" section #17b
          http://www.phy6.org/stargaze/Smasscom.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:             ....stargaze/Lintro.htm

• Learn to distinguish between weight and mass. Both are properties of matter, and all observations suggest that they are proportional to each other. Weight is the force by which an object is attracted by gravity. Mass is the extent to which it resists acceleration.

• Learn that in oscillations of a mass against an elastic spring--in the absence of gravity, or in horizontal motion--the length of the oscillation period is proportional to the square root of the mass. This makes it possible to compare masses without the use of gravity.

• Learn about space station Skylab and the measurement of astronaut mass conducted aboard it.

Terms: mass, weight, inertia, zero-g

Stories and extras: The story of Skylab and studies of weight-loss by its crew members.

Hands-on activities: A simple experiment with a clamped hacksaw blade, containing some elements of the Skylab measurements.

1. These linked sections are relatively free of mathematics, because they stress the intuitive distinction between weight and mass, a subject on which many students and even some teachers are unclear. It is hoped that the distinction is made clear by approaching it in more than one way, and illustrating it by as many examples as possible.

2. Some teachers still maintain that a two-pan balance measures weight, while a spring balance measures mass. This is misleading and should be avoided: both devices rely on gravity, and therefore both measure weight.
     The way they do so differs. The two-pan balance compares the weight of the object being examined to that of a set of standard weights in the other pan. The spring balance, on the other hand, compares that weight to the pull of a calibrated spring.

     Thus on the Moon, where gravity is only 1/6 of its value on Earth, the spring balance will record a smaller weight, but the two-pan balance will not. That is because on the Moon, the pull of the spring is unchanged, but the balancing weights in the other pan also weigh only 1/6 of what they weigh on Earth. In both cases, however, what is measured is weight, not mass, because gravity is involved.

   ---

   Starting out:Today we will discuss two concepts which often get confused--weight and mass. Many students feel that, since both are measured in kilograms or pounds, both are really the same thing.

   (Write the following on the board)

   Actually, weight and mass are two different properties of matter:
   Weight causes motion, it is the force due to gravity.

   Mass resists motion.

   We should exclude here motion without acceleration, which by Newton's first law can continue by itself indefinitely.
   So, more accurately:
   Weight can cause acceleration.

   Mass resists acceleration.

   (End of words copied from the board)

     Galileo showed by experiments that (disregarding air resistance) big stones fell no faster than small ones. But why? If they were pulled down by a stronger force, why didn't they fall any faster?

     Newton guessed the reason. All material also resists acceleration. A big stone with 10 times the weight of a small one also has 10 times the resistance, and therefore it does not fall any faster. Newton named the resistance to acceleration intertia. We call it mass.

     If the only use of the concept of mass was for explaining why big and small stones, in free fall, accelerated at the same rate, it would not be very useful. However, there also exist many motions in which gravity plays no role--horizontal motions on Earth, and motions in "zero g" in space. Weight does not drive such motions, but inertia remains an important factor. For instance...

   Continue with examples from the lesson, of a rolling bowling ball and a rolling wagon--both starting their motion and stopping it.

   Additional examples: we read about train locomotives hitting cars which stalled on railroad tracks, because those trains were too massive to stop quickly.

   Supertankers (aka "large crude oil carriers"), ships of 200,000 tons and more, are even harder to stop when fully loaded, taking several miles to do so.

     On the other hand, when we need to accelerate and stop pieces of material quickly, they better have a very low mass. The tiny metal slugs which push the ribbon in matrix printers for computers (now driven out by laser printers and ink-jet printers, though they are still used in industry to mark merchandise) are very light and can therefore hit and rebound very rapidly.

     Then go over Skylab story. As a project, some students may prepare a presentation on Skylab, based on the October 1974 article about it in "National Geographic." All past issues of that magazine are available on compact disks, or in paper copies in libraries.

     The hands-on experiment in section (17b) may be performed as the teacher chooses--together with the Skylab discussion, before it or afterwards.

   ---

   Guiding questions and additional tidbits with suggested answers.

   ---

   -- What is the difference between the mass and weight of a bowling ball?
   The ball has both weight and mass. Its weight makes it hard to lift. Its mass makes it hard to get rolling, and also hard to stop.

   ---

   --What do we mean by the ball's weight?
   Its weight is the force by which gravity pulls the ball down.

   ---

   -- What do we mean by the ball's mass?
   The ball's mass is its inertia, its resistance to acceleration.

   ---

   -- Suppose that some time, in the far future, a bowling alley is built on the Moon, where gravity is 1/6 of what it is on Earth. Would it be easier there to roll the ball down the alley?
   It would be easier to lift the ball off the floor, but not any easier to get it rolling.

   ---

   --An astronaut in a space suit, in the space shuttle bay, tries to push a one-ton scientific satellite out of the bay, but the satellite proves very hard to move. If it is weightless, why should it be so?
   It has no weight, but it has one ton of mass.

   ---

   --Should the astronaut give up trying to push it?
   Not necessarily. If he keeps pushing it will accelerate--it just does so very slowly. In a minute it might be moving fast enough to float out of the bay. At this point, however, the astronaut better be ready to let it float away--trying to stop it would be just as hard!

   ---

   --On Earth we drop from a high point a bowling ball and a marble. The marble has only 1/1000 of the weight of the ball, but it falls just as fast. Why?
   The marble also has only 1/1000 of the inertia or mass of the bowling ball. By Newton's law

   a = F/m

   Both F and m for the marble are 1/1000 times less, but their ratio is the same as with the bowling ball, and therefore the marble accelerates at the same rate.

   ---

   --If the Earth's gravity reaches up to the Moon (which is held by it), how can we have a "zero gravity" environment aboard a space station that orbits a mere 300 miles above ground?
   Gravity does act on the space station, too--that is what keeps it in its orbit. In fact, gravity is the only external force acting on it and on the astronauts inside (same as it is in free fall).

   That means that inside the station, no additional force pulls objects towards Earth. In the reference frame of the space station it feels like "zero g", because no outside force is evident. ["Stargazers" returns to this matter in a later section, where frames of reference are discussed.]

   ---

   --Before electronic wrist-watches were introduced (around 1980), mechanical ones were used. How were they designed, to operate in any position?

   They obviously could not depend on gravity, so they too used a spring and an oscillating mass. The mass was a balance wheel, which rotated back-and-forth against a spiral spring.

   [It might be possible to show the class an old mechanical alarm clock with its back removed, provided the balance wheel is clearly visible, which often is not the case.]

   ---

   (Questions about the "Skylab" section, #17a)

   --How can mass be measured in "zero g"?

   By tying the mass to a spring, pulling it a little in one direction and measuring the period of oscillation. The force of the spring only depends on the extent to which it is stretched or compressed--gravity plays no role. The oscillation however becomes slower--and its period longer--the greater the mass that is being moved.

   (It can be shown that the period is proportional to the square root of the mass.)

   ---

   --How was astronaut mass measured aboard Skylab?

   --What did measurements of astronaut mass aboard Skylab reveal?

   ---

   (Question after the experiment in section #17b)

   -- Suppose the same hacksaw blade described in the author's experiment in section #17b was also used in the mass-measuring device aboard Skylab. If the device carried an astronaut known to weigh about 70 kg, what would be its back-and-forth period?

   In the notation of that section, for m₁ = 50 gr., the blade gave a period T₁ of 0.5 seconds. If m₂ = 70 kg, m₂/m₁ = 1400, SQRT(m₂/m₁) = 37.42, multiply by T₁ = 0.5 sec to give T₂ ~ 18.7 seconds.

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:             ....stargaze/Lintro.htm

• A version of Newton's laws of motion without the concepts of mass and force.

• How that formulation of Newton's laws allows mass and force to be defined, and about their units, the kilogram and the Newton.

• To apply and use F = ma to motion caused by gravity.

• The distinction between gravitational mass and inertial mass.

• That if an object is at rest, that does not mean no forces act on it--just that all forces on it add up to zero. If a book on the table does not fall, this does not mean gravity has stopped pulling it--just that the table also exerts a force, and that the sum of that force and the book's weight adds up to zero.

Starting out: (underlined statements below may be put on the blackboard, to be copied by students.)   We have so far discussed Newton's laws in a general, intuitive way. We have given:

--Their formal wording--3 laws

--The meaning of the 1st law

--"without the action of forces, motion in a straight line at constant speed continues indefinitely"

--The meaning of the 3rd law

--"Forces occur in pairs, same magnitude, opposite directions"

--The meaning of mass

--"Resistance to acceleration, inertia"

  We could of course define force by weight, using gravity. But if we do, all our calculations will depend somehow on the constant of gravity, on g--it could be done, but we are looking for a cleaner way.

  We have also discussed the idea of mass, but we still need a good way of measuring it. One could use the hacksaw-blade formula--but we have not yet reached the point where that formula can be derived!

(on the board) How do we measure mass?

  We will address these problems in the way of Ernst Mach, who lived two centuries after Newton. Here is what we will do:

(on the board)
Solution: Formulate Newton's laws using neither "force" nor "mass."

Continue with the "Stargazers" material.

Review:
What does Newton's first law say?
What does Newton's second law say?
What does Newton's third law say?

When two compact objects ("point masses") act on each other, they accelerate in opposite directions, and the ratio of their accelerations is always the same.

The newton is the force that can give 1 kg of mass an acceleration of 1 meter/sec².

When you jump from a high place, gravity gives your body an acceleration of g=10 m/s². Your weight is therefore 700 newtons.

This is a tricky question, related not only to F=ma but also to the concept of equilibrium, discussed at the end. An unthinking application of Newton's second law would give
a = F/m = 240,000/12,000 = 20 m/s2 = 2g

but is wrong.

Before launch, the rocket's weight is supported by the launching pad. Its weight is 12,000 g = 120,000 newton and since it does not move, an equal and opposite upward force of 120,000 newtons is exerted on it by the pad from below.

At the lift-off moment, that force ceases to act on the rocket: instead, the thrust of the engine now supports the rocket's weight (and if the engine generates a thrust smaller than the weight--less than 120,000 newton--the rocket will not lift off). So that force must be subtracted from what is available to accelerate the rocket. The result is

a = F/m = (240,000 - 120,000)/12000 = 10 m/s² = 1 g

The total mass left is 3000 kg, the total weight is 30,000 newtons, so a = F/m = (240,000 - 3000)/3000 = 210,000/3000 = 70 m/s² = 7g.

Probably astrite. Balls of equal size and shape of the two materials are equally hard to lift, but astrite needs a greater force to get started and therefore delivers a greater force to the pins.

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:             ....stargaze/Lintro.htm

Goals: The student will learn

• The concepts of momentum and its conservation, using the recoil of a cannon as an example.

• That momentum is a vector, allowing its conservation to be applied to problems in 2 and 3 dimensions.

• That in the recoil of a gun, momentum is shared equally, but energy is not.

• An example shows that, similarly, in collisions kinetic energy needs not be conserved.

Terms: momentum, conservation of momentum, recoil.

Starting the lesson:
Underlined statements may be put on the blackboard, to be copied by students.

  We have discussed so far mass, velocity, acceleration, force and energy, and the way Newton's laws tie them together.
  There exists one additional concept which is rather important, namely,

momentum P = mass times velocity

In an isolated system, momentum is conserved.

  Now you already know that energy is conserved, but there exists a big difference: energy can change into other forms, say turn into heat. Therefore

mechanical energy, (potential + kinetic), is not always conserved--some of it may change into other forms.

[In passing, that is how armor-piercing shells are designed. They can work their way through 4 inches (10 centimeters) or more of steel in a tank's armor, not by smashing the steel, which is too strong, but by melting it. Such shells usually contain a core of tungsten or uranium ("depleted uranium" from which the component used for producing nuclear power has been removed), very heavy metals whose high mass can also carry a great deal of kinetic energy.]

The total momentum going (say) into a collision always equals the total momentum coming out of it--there is nothing else momentum can convert to. It is therefore something we can always rely on in a calculation. The momentum given by a rocket to its gas jet is always equal to the momentum which it itself receives, regardless of the details of the process.

  The way momentum will be introduced here is through an actual example.

Here go into the lesson, the calculation of the recoil of a cannon.

P = mv

Yes, momentum is a vector quantity. If all motions are along the same line, we can take vector character into account by giving momenta in one direction a (+) sign and in the opposite direction a (-) sign.

In an isolated system, the sum of all momenta is conserved.

A system with no forces acting on it from the outside.

When you jump, you brace your foot against the ground, so that the Earth, too, is part of the system. When your body takes off, an opposite and equal amount of momentum has been given to the Earth, and in principle the Earth actually moves back a tiny, unmeasurable amount. When you land, your momentum is given back to the Earth, and everything is as before.

Let 1 denote the car, and let the + direction be the one in which it moved.
Let 2 denote the truck, moving in the - direction.

For the equations of the conservation of momentum, the units are not important, as long as the same ones are used before and after the collision (i.e. as long as we compare quantities measured in the same units).

So:

m₁ = 1500 kg    v₁ = 40 km/s
m₂ = 4500 kg     v₂ = -20 km/s

P = m₁v₁ + m₂v₂ = (m₁ + m₂)v₃

1500*40 + 4500*(-20) = 60,000 - 90,000 = -30,000 = 6000*v

v = - 5 km/s

Not likely, since each of the masses (if we consider them separately after the collision) now moves more slowly than before.

If the result is to be expressed in joules, we better convert km/hr to meters/second:

1 km/hr = (1000 meter/3600 sec) = 0.27777 m/s

Initial velocities: v₁ = 11.111 m/s   v₂ = 5.5555 m/s
Final velocity     v₃ = 1.3889 m/s

Kinetic energy =1/2 m v²

KE of the car         (1/2) 1500 (11.111)² = 92, 593
KE of the truck     (1/2) 4500 (5.5555)² = 69,444 joule

Total kinetic energy entering the collision 162,037 joule
Final KE (1/2) 6000 (1.3889)² = 5,787 joule
Loss = 156,250 joule

---

--Where did the lost energy go?
It probably went into heat.

---

--(Optional) Humongous airlines publicized the smooth ride of its new "steadijet" airliner by installing a billiards table in its first class cabin. While the plane is flying at a steady velocity v₀, do collisions of two billiard balls in it conserve momentum?
Yes, they do

---

--Which velocities do we have to use in such a calculation--velocities relative to the airplane or to the ground? (For simplicity, assume the balls collide head-on and move along the direction in which the airplane flies, so that all motions are along the same line.) '
It makes no difference. Suppose the colliding billiard balls have masses (m₁, m₂) and viewed from the airplane ("in the reference frame of the airplane") have velocities (v₁, v₂) where v₁ is positive and v₂ negative. The balls bounce back at velocities (v₁ ',v₂ ') and the conservation of momentum gives
m₁v₁ + m₂v₂ = m₁v₁ ' + m₂v₂ '

Viewed from the ground, each velocity is increased by the velocity v₀ of the airplane, so the conservation of momentum should give
m₁(v₁+v₀ ) + m₂(v₂+v₀) = m₁(v₁ '+v₀) + m₂(v₂ '+v₀)

This equation differs from the one preceding it only in having m₁v₀+m₂v₀ added to both sides. Since equations remain valid when equal quantities are added on both of their two sides, if one of these equations holds, the other automatically does so, too.

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index:             ....stargaze/Lintro.htm

• About uniform circular motion, and the relation of its frequency of N revolutions/sec with the peripheral velocity v and with the rotation period T.

• That uniform circular motion is a type of accelerated motion.

• That the "centripetal acceleration" of an object going around a circle of radius R with constant speed v equals v²/r and is directed towards the center of the motion.

• An elementary proof of the preceding result, using the theorem of Pythagoras. The proof depends on neglecting a small quantity x, but because x can be made as small as we please, it holds exactly.

• That intuition can deceive. Even though an object whirling around a circle strains to pull away from the center, if it is cut loose, it will not move in that direction, but will continue along a straight line tangential to the circle.

Terms: uniform circular motion, frequency, peripheral velocity, centripetal acceleration and force.

Starting out:  Today we will learn about the simplest case of motion not in a straight line, uniform motion around a circle. Of course, that is an accelerated motion, because by Newton's first law (or at least, by what that law implies), any motion not in a straight line is accelerated, and requires a force for maintaining it.

(Illustrate the following by a drawing on the board, to which details are added as the discussion progresses.)

[If a students says "because of the centrifugal (or centripetal) force," say "that is just a word, a technical term. What is actually happening?"]

  The string does not allow it to do so, but pulls it back towards your hand, to keep it in its circle. We will show today that motion in a circle can be viewed as the combination of two motions taking place at the same time--like the motion of the airplane, flying in a cross-wind (Section #14).

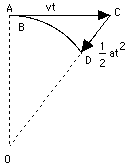  One motion is the continuation of the existing velocity along a straight line (show on the drawing)--the way the weight would move by Newton's first law, if no outside force acted on it.

  The other is a motion towards the center of the circle (draw it, too), returning the weight to its circular path. (Figuratively returning it; in actuality, both motions are simultaneous and the weight never leaves the circle.) That second motion, it will be shown, is an accelerated one...

  Now for the details..... (Continue on the board with the derivations, while the students copy into their notebooks.)

(Suggested answers, brackets for comments by the teacher or "optional")

The speed, the magnitude of the velocity, is indeed constant. But the direction changes all the time. Velocity is a vector quantity, and any change of its direction also involves acceleration.

It continues along a straight line, tangent to the circle in which it moved.

Because from the moment when it is released, no forces exist any more in the direction of the string. The stone strains against the centripetal force only as long as it moves in a circle.

Along a line tangent to the wheel. If, as is likely, the mud flies off soon after the wheel has picked it up from the road, it will fly backwards and upwards from the rim of the wheel--in the direction of the mudguards which truckers hang behind their wheels to intercept it.
[Draw schematic on the blackboard].

v²/r, directed to the center of the circle.

No, it is exact, because x can be made as small as we please.

T = 1/N. The total time spent in those N circuits is found by multiplying the number of circuits (=N) by the length of each one (=T). But that time, by definition, is one second, so NT = 1 from which T = 1/N.

The distance covered in each revolution is 2pR The distance covered in one second is (2pR)N--which by definition is also its peripheral speed. Hence
a = (2pRN)²/R = (2pN)² R²/R = (2pN)² R

Astronauts are subjected to large accelerations during launch and re-entry. The forces associated with such accelerations are often called "g forces" because they are measured in gravities, i.e. the acceleration is measured in units of g, the acceleration due to gravity for which we will use the approximate value 10 m/sec².

In another lesson in "'Stargazers" it was noted that the V2 rocket of World War II started with an acceleration of 1 g and ended at "burn-out", with its mass (mostly fuel) greatly reduced, at about 7 g. The space shuttle (I believe) pulls 3g before burnout, which is quite uncomfortable, even for someone lying flat on the back on a contoured surface. Re-entry has comparable (negative) accelerations.

To get astronaut used to taking such forces, they are whirled around during their ground training in a centrifuge, inside a small cabin mounted at the end of a horizontally rotating arm. (Anyone seen such centrifuges on TV?) They are a bit like some amusement park rides, but can create greater stresses, and have TV cameras that monitor the rider.

Taking g = 10 m/s²,

10 = (2pN)² R = (6.28)² N² (6) = 236.63 N²
N² = 0.04226
N = 0.206 rev/sec (larger than N², of course, since N<1 !)
T = 1/N ~ 5 seconds

It will be 4g, since it grows like the square power of v (or of N).

That is the force keeping the astronaut moving in a circle. It is transmitted to the astronaut's body by the chair or couch that supports it.