Lesson Plan #30 http://www.phy6.org/stargaze/Lgravity.htm

(20) Newton's Theory of Universal Gravitation

This lesson re-derives Newton's result, that if the force of gravity decreases like the square of the distance from the center of attraction, the same force that causes objects on the Earth"s surface to fall can also be responsible for the motion of the Moon.

Part of a high school course on astronomy, Newtonian mechanics and spaceflight
by David P. Stern, Code 695, Goddard Space Flight Center, Greenbelt, MD 20771
u5dps@lepvax.gsfc.nasa.gov or audavstern@erols.com

This lesson plan supplements: "Newton's Theory of Universal Gravitation," section #20 http://www.phy6.org/stargaze/Sgravity.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Goals: The student will learn

How Newton tied together the gravity observed on Earth and the motion of the Moon.

To apply an earlier lesson about centripetal forces.

To appreciate the philosophical implication of Newton's calculation: all parts of the universe seem to obey the same laws of nature.

Terms: Gravitation (or gravity), inverse-square law, solar constant.

Stories: The Story of Newton's apple is traced to its source. Also, mention is made of Cavendish and Eötvös (and in this lesson plan, of Coulomb).

Starting the lesson:

Today we will learn about Newton's theory of universal gravitation. The story is often told that Newton was inspired to this by a falling apple--with some going so far as to suggest it bonked him on the head as he was sitting under a tree. We will come back to that story.

Of course, Newton did not "discover" gravity. People in his time were well aware that the Earth attracted all objects near its surface, and Galileo, as you learned some time ago, experimented with falling objects. But all these observations had to do with what happened close to Earth, in a region accessible to experimenters. The objects in the sky--planets orbiting in space, the Moon circling around the Earth--seemed to belong to a different class of phenomena, with separate rules, such as Kepler's laws. Astronomers were only beginning to understand those phenomena.

Newton's achievement was in making the connection, in proposing that the same force that pulled apples down also pulled the Moon.

Suppose, he said, that the force decreased like the square of the distance from the center of Earth. The Moon is 60 times more distant than the surface of the Earth, so the force of gravity should be 60 times 60, or 3600 times weaker. Would that equal the centripetal force mv²/R or 4p²N²R needed to hold the Moon in its orbit?

Newton could calculate that--he knew R from Aristarchus and Hipparchus, and he knew N = 1/T, where T was the orbital period of the Moon. As you will see, the result fit well, and Newton concluded that it was indeed the gravity of the Earth that held the Moon to its orbit. He also guessed (correctly) that the Sun had a force of gravity much like the Earth's, and that was what kept the planets going around it. That is why he named his idea the theory of universal gravitation.

Was the inverse squares law just a lucky guess? It was more. Imagine a source of light--say, the Sun--shining at equal intensity in all directions, sending out each second sunlight carrying an energy of I joules--that is, radiating a power of I watts. What is the density at which solar power flows at a distance of R meters, across an area of, say, 1 square meter (1 meter²)?

A sphere of radius R centered on the Sun has an area 4pR² meters². Since all parts of the sphere receive equal illuminaton, each square meter receives a power I/4pR² watts, and obviously, that intensity decreases like 1/R2. At Earth's orbit it equals 1360 watt/m², a quantity known as the solar constant. At the orbit of Jupiter, R is about 5 times larger, and the light intensity is only 1/ 5² = 1/25 of the solar constant, which is why Pioneers 10 and 11, and Voyagers 1 and 2, preferred a power source other than solar cells. And although a lightbulb does not shine with equal intensity in all directions, your reading illumination, too, will decrease approximately like the square of the distance from it.

By the way:

radiation.

also

even though the two phenomena are different and unrelated.

Students should be made aware that the damaging kinds of radiation are the ones also known as ionizing radiation, "ionizing" meaning they deliver enough energy to atoms and molecules to tear off electrons. These can be fast ions and electrons from radioactivity, or high-energy "electromagnetic" radiation similar to microwaves, radio waves and light, but of the types known as x-rays and gamma rays.]

Newton was aware of such results, and the 1/R² law was a natural assumption for him. Today that calculation is easy to repeat--but remember, one needed at least some idea of the laws of motion and of the centripetal force which they prescribe. Galileo and Kepler lacked that knowledge, and could not have tested the 1/R² law without it.

Newton's "universal" gravitation led to a principle which today is all too easily taken for granted: that the same physical laws hold anywhere in the universe. All the astronomical evidence since Newton's time seems to confirm it: not just the laws of gravity, but the chemical elements, the speed of light, the way light is produced and other physical processes seem to be the same on Earth and in distant stars, or even in other galaxies.

Now let us go back to that apple. (Continue with the original story of Newton's apple as given in "Stargazers").

Questions to ask
Since the entire lesson focuses on a single calculation, not much can be asked beyond its details.

What idea did the falling apple supposedly inspire in Newton?

--That the force of gravity which causes objects to fall was also the force that kept the Moon in its orbit around Earth.

What did Newton have to assume, to test his guess?

--He had to assume something about the rate at which gravity decreased with distance. His assumption was an "inverse square law"--that gravity decreased like 1/R².

Concluding comments (Optional)

The French military engineer Augustine Coulomb lived a century after Newton. In 1777 he won a prize for a new method to measure the Earth's magnetism--by suspending a horizontal bar magnet by its middle, from a long string, with a pointer attached--or better, a small mirror (draw on the board). When a beam of light is reflected from the mirror, even small magnetic variations can be measured, even those that twist the magnet by just a tiny amount from its quiet position.

Coulomb also adapted this "torsion balance" instrument to measure the force between two magnetic poles--either repelling or attracting. You bring the pole end of a second bar magnet near one of the poles of the suspended magnet. The force between them can then be measured by the twisting of the suspension string, which exerts an elastic force. Coulomb found that magnetic poles, like gravity, attracted and repelled with a force that decreased like the inverse of the square of the distance.

Coulomb's experiment was so sensitive that static electricity, which generated its own forces, sometimes interfered with its observations. That gave Coulomb the idea of measuring electric forces the same way. He replaced the magnet with a little dumb-bell shaped stick, with small spheres at the end. He then charged one sphere with static electricity, brought close to it another charged sphere, and measured the force. Guess what? Electric forces also decreased like 1/R².

A reclusive English gentleman named Henry Cavendish set out to use the same method to measure the force of gravity directly. Instead of two lightweight spheres at the end of the stick, he used two heavy ones, and attracted one of them by a third sphere, a big one. The force was tiny and because of the big masses, the instrument reacted agonizingly slowly. But in 1796, he finally succeeded--showing that not just the sphere of the Earth, but even spheres of lead in the lab, exerted a measurable force of gravity.

Lesson Plan #31 http://www.phy6.org/stargaze/Lkepl3rd.htm

(21) Kepler's 3rd Law

(21a) Application of Kepler's 3rd Law

In these closely linked units, Newton's calculation is applied to artificial Earth satellites. It is shown that at least for circular orbits, this calculation leads to Kepler's 3rd law. The velocity required for a low Earth orbit is derived, and a practical formula is obtained for the orbital period in a circular Earth orbit of any radius.

This lesson plan supplements: "Kepler's 3rd Law," section #21 http://www.phy6.org/stargaze/Skepl3rd.htm

"Application of Kepler's 3rd Law," section #21a http://www.phy6.org/stargaze/Sappl3rd.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Goals: The student will learn

To derive the velocity in a circular orbit of any radius.

To derive the Earth escape velocity.

To prove Kepler's 3rd law for circular orbits

A simple formula for the orbital period in a circular Earth orbit of given radius.

Terms: Orbital velocity, escape velocity, synchronous orbit.

Starting the lesson:

Today we will apply Newton's calculation to circular Earth orbits. As already noted, all three of Kepler's laws can be derived from an inverse-square gravitational force, assuming only that it acts primarily between only two bodies--e.g. Sun and planet, Earth and Moon--while the pull of all others can be neglected.

With our limited math we can handle here only circular orbits, not elliptical ones. Circular orbits are a somewhat special and simple case. The first law for instance is automatically satisfied, because yes, the circle is an ellipse--of zero eccentricity and with both its foci combined at the center.

The second law alsodoes not add any information about the motion. The speed of a satellite or planet in a circular orbit is constant, and so is its distance from the center. The area swept by the radius per unit time is then automatically constant.

The third law, however, is meaningful even for circular orbits. Newton's calculation allows it to be checked, and today we will show that the inverse-squares law indeed gives the expected result.

In this day and age we are interested not just in planetary orbits but also in the orbits of artificial satellites. We will therefore use such orbits to illustrate the calculation, and some useful results will also be derived.

Let us start by calculating the velocity v₁ required by a spacecraft in a circular low Earth orbit--what is called in Russia "the first cosmic velocity."

[Go over lesson 21, mentioning that what we call "escape velocity" is called in Russia the "second cosmic velocity."]

Questions and worked examples

This section is again mostly concerned with one calculation, and the questions asked are all related to it.

Express the orbital velocity v₁ at r = 1 R_E, given the acceleration of gravity at that distance as g = 9.81 m/s2 and the radius of the Earth R_E = 6,371,000 meters.

This derivation is found in lesson 21)

If you give the above velocity v₁ to a rocket launched vertically, straight up, how far from Earth will it get before falling back?
Hint: the semi-major axis of an orbit depends only on the energy.

Since the energy is the same as the one required for low Earth orbit, the semi-major axis a will also be the same. For the low Earth orbit, a = 1 R_E, hence the same value holds here, too, making the ellipse 2R_E long. The highest point of the trajectory--the apogee of the orbit--will therefore be at the height of 1 R_E above ground.

Given the orbital velocity for a circular orbit at 1 R_E as 7.9 km/sec, what is the escape velocity at the surface of the Earth (r = 1 R_E)?
What sort of "escape" does it provide, and what sort doesn't it?

₂

If an object above the atmosphere has a velocity greater than the escape velocity v₂, in what upward direction must it move to escape the Earth's gravity?

It does not matter. An escape orbit is the limiting case of an orbit with very, very large semi-major axis, and therefore a very distant apogee. With a starting speed close to the escape velocity, in whichever upward direction the object is moving, its starting point is always close to the perigee, and it is always headed for the apogee. In the limit (=at escape velocity), this means it is heading for infinity.

The Earth orbits the Sun in a near circular orbit of radius 1 AU (Astronomical Unit) at 30 km/sec. How much extra velocity, above and beyond 11.2 km/s, does a spacecraft escaping the Earth's gravity need, to escape the Sun's gravity as well?

_2s

In some weird alternate universe (already met in the lesson on Newton's 2nd law) weight and mass are not proportional. Two materials, astrite and barite, have the same weight per unit volume, but a volume of astrite has twice the mass of a similar volume of barite.

Both are strong and light metals, and are a natural choice for spacecraft construction; we can assume that barite behaves the way aluminum does on Earth. Which of the two would be a better choice?

mg/R² = mv²/(R_E R) and hence v² = g R_E/R

An astrite satellite has the same weight but twice the mass, so Newton's equation becomes

mg/R² = 2mv²/(R_E R) and hence v² = g R_E/2R

The orbital velocity required by the astrite satellite at distance R is therefore smaller by a factor SQRT(2) = 1.4142 than that of a barite satellite in the same orbit, making astrite the obvious choice.

--The planet Mars has a radius of R_M=3390 km and its satellite Deimos orbits it in a near-circular orbit with orbital period T_D = 1.26244 days and a mean distance of R_D = 23,436 kilometers. What is (1) The acceleration g_M due to gravity at the surface of Mars and (2) The escape velocity there?

g_M (R_M/R_D)2 = v²/ R_D

where v is the velocity of Deimos in its orbit. From a previous calculation, if N is the number of orbits per second and T_D is also given in seconds

v = 2pR_DN = 2pR_D/T_D

T_D = 1.26244*86400 sec = 109,075 sec.

v = 6.2832*(23,436,000 m)/109,075sec = 1350 m/sec

In calculating a ratio we can use kilometers, so R_D/R_M = 23,436/3390 = 6.9133

We then have

g_M = v²R_D/R_M² = (v²/R_D) (R_D/R_M)²

g_M = ((1350)²/23,436,000)*(6.9133)² =

= 0.077764*47.793 = 3.717 m/s²

i.e. slightly more than 1/3 the acceleration of free fall on Earth. The orbital velocity V_1m at the surface of Mars, in analogy with V₁ derived for Earth, is found from

V_1m² = g_M R_M = 3.717*3,390,000 = 12,600,000

V_1m = 3549.6 m/s = 3.5496 km/s

The escape velocity is SQRT(2)=1.4142 times that, or 5.02 km/sec.

According to Kepler's 3rd law, T is proportional to a, where T is the orbital period in seconds and a the semi-major axis in meters. That implies T² = ka³ . In a circular orbit around Earth, a=r where r is the orbital radius. Can you derive k for such orbits?

The result is derived in "Stargazers" and is k = g R_E/4p²

Here the teacher may continue with lesson 21a (which is optional). Some questions related to that lesson:

From Kepler's 3rd law, the orbital period T around Earth in a circular orbit at distance R is

T = Q *R*SQRT(R)
If R is given in Earth radii, what is the value of Q?

The calculation in "Stargazers" gives 5063.5 seconds.

--At what distance R is the orbital period around Earth 24 hours? Why is that orbit important?

^3/2

R^3/2 = 17.0633 R = (17.0633)^2/3 = 6.628 R_E

The orbit is important because a satellite in an equatorial orbit at this distance stays all the time above the same point on the Earth's equator, and rotates with the Earth as if it were attached to it by a rigid rod. That makes such a"synchronous orbit" desirable for communication satellite, because they can then be tracked from the ground by a fixed antenna.

--Navigational satellites of the GPS (Global Positioning System) move in 12 hour orbits. What is their distance?

--The calculation is very similar to the preceding one.

We have 43200 sec = 5063.5 R*SQRT(R) = 5063.5 R^3/2

R^3/2 = 8.53164 R = (8.53164)^2/3 = 4.175 R_E

Lesson Plan #32 http://www.phy6.org/stargaze/Lframes1.htm

#22 Frames of Reference: The Basics

#22a The Aberration of Starlight

#22b The Theory of Relativity

Velocity and acceleration always need to be measured relative to some fixed benchmarks, which define a "frame of reference. " Do the laws of physics depend on which frame we use? This section shows that two frames of reference moving relative to each other with a constant velocity are completely equivalent, and the same laws hold in both.

Each such frame is consistent, but their observations may differ. Section 22a describes how the motion of the Earth modifies the apparent positions of stars and the arrival direction of the solar wind.

Optional Section 22b contains a brief non-mathematical discussion of what the theory of relativity is about.

This lesson plan supplements:
  "Frames of Reference: The Basics," section #22 http://www.phy6.org/stargaze/Sframes1.htm
   "The Aberration of Starlight," section #22a        http://www.phy6.org/stargaze/Saberr.htm
   "TheTheory of Relativity," section #22b
http://www.phy6.org/stargaze/Srelativ.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Goals: The student will learn

The concept of frames of reference in physics.
That two frames of reference, each moving with respect to the other with a constant velocity v (constant speed, constant direction), observe the same accelerations and therefore Newton's laws are the same in both.
About the aberration of starlight and its explanation by James Bradley, including the story of the flag on a moving boat, which gave the essential clue.
About the aberration of the solar wind and the behavior of comet tails.
About the proposed "Solar Probe" space mission
(optional sect. 22b) What Einstein's theory of relativity is about, in qualitative terms.

Terms: frame of reference, relative velocity, stellar aberration, solar wind, comet tails, principle of relativity, classical mechanics, relativistic mechanics, quantum mechanics.

Stories and extensions: The story of the aberration of starlight and of Bradley's observation on a boat in the river. About the solar wind, magnetosphere and comets.

Note to the teacher: This lesson is closely related to the one on vectors (section #14 of "Stargazers", lesson plan #23). Some ideas expanded here were already introduced in #14--for instance, the motion of an airplane flying with velocity v₁ relative to the air, which itself (because of the blowing wind) has a velocity v₂ relative to the ground. In that example, the air and the ground represent two frames of reference moving with respect to the other, and we have already shown that the velocity of the airplane with respect to the ground is the vector sum v₁+v₂ .

Here, however, two additional aspects come into play. One, we are also concerned with accelerations and forces. These are the simplest cases, where all velocities are constant in magnitude and direction, so that shifting from one frame to the other adds no new forces or accelerations (That will no longer hold when we come to discuss rotating frames). . And two, we study the changes created by the motion of the observer's own frame of reference.

Section (22a) is optional. It contains interesting stories, illustrating the lesson, but can be omitted (and perhaps assigned to some advanced students) if time runs short. It is also possible to teach only the first example, on the aberration of starlight and on its explanation by James Bradley.

Starting the lesson.

The starting paragraphs of Section #22 are quite appropriate for starting the lesson. After that, bring up the questions below, and continue with Section #22a.

Questions and tidbits:

--What is meant by a "frame of reference"?

A frame of reference is a set of reference points with respect to which motion is measured. These points move together and keep their relative distances and angles of view.

--Can you give examples of frames of reference?

We have two frames of reference: A is the inside an elevator rising with constant velocity u, B is the frame of the building in which the elevator is located. A rider drops a penny inside the elevator. Is the velocity of the penny the same as seen from A and B?

falling

rising

In the preceding example, is the acceleration of the penny the same viewed inside the elevator and outside it?

--Yes, it is equal to g in both frames--as long as the elevator's velocity is constant.

You are the passenger in a car driving with velocity u on a rainy night. On the street outside, through the side window of the car, you see raindrops falling. They fall with a constant velocity v (because of air resistance, they no longer accelerate). As you watch them in the light of streetlights, how do they appear to move? What is their apparent velocity w? In what direction do they streak the windows?

-u

(Draw on the board)

Their velocity vector w has a vertical downwards component v (magnitude of v) and a horizontal component u (magnitude of -u) to the rear: in vector notation w = v-u = v+(-u). Since v and u are perpendicular to each other, by Pythagoras, w = SQRT(v² + u²). Their streaks on the window are in the direction of w and the angle A between those streaks and the vertical satisfies sinA = u/w or tanA = u/v.

How are distances to stars measured by the parallax method?

If the directions to C are slightly different when viewed from A and B, then the difference gives the "parallax" angle between AC and BC. Using that angle one can calculate all other properties of the triangle ABC, including the distances AC abd BC from Earth to the star.

What changes were observed around 1700 in the position of Polaris?

It seemed to move in a small ellipse, about 20" wide.

How did astronomers know that it was not Polaris that did the moving?

The motion around the ellipse took 1 year to complete, and it was highly unlikely that Polaris would match the Earth's orbital period. Also, other stars near Polaris displayed similar motions.

--How did James Bradley know that the shift of Polaris was not a parallax effect?

Because the greatest displacement of Polaris in any direction did not match the greatest displacement in the opposite direction by Earth in its orbit, but occured 3 months afterwards.

--In the end, how did Bradley explain the strange shift in the position of Polaris and other stars?

-u

--The aberration of starlight allows us to deduce that the Earth is indeed moving. Doesnŝt that contradict an earlier claim that absolute motion is undetectable?

with constant velocity in a straight line

[Optional further discussion by the teacher:

did

Actually, we have other cues, and from them we know that the solar system is moving at about 20 km/s towards a point known as the solar apex, near the star Vega. But in principle, it could also be that we are at rest and all those stars are moving in our direction, away from the solar apex. The physical effects would be exactly the same. It is only our logic that tells us it is more likely that our sun is moving, rather that a large number of distant suns happen to move on parallel tracks.]

[Harder poser--perhaps to take home] How do you think would a star on the ecliptic appear to move? Hint: it's not a circle--not even close!

Why does the solar wind, on the average, appear to come not from the Sun but from a direction 4 degrees off the Sun?

-u

You are aboard a steamship traveling at velocity u while the wind blows at velocity v. From your point of view, at what velocity does the smoke seem to travel?

-u

v-u

-u

How is the plume of smoke from a steamship similar to the tail of a comet?

The difference is that the comet releases two kinds of "smoke, " namely dust and plasma. Each of them responds to a different "wind". The dust responds to sunlight, whose velocity c is much greater than u, so in the frame of the comet, that light essentially arrives in its original direction, radially from the Sun. The dust tail is then stretched out radially too (even though its velocity, to be sure, is much smaller than c).

The solar wind also moves radially out, but its velocity v is only some 4-6 times larger than u. As a result, the plasma tail which it affects moves at v-u relative to the comet and makes an appreciable angle with the radial direction.

What do you know about the "Solar Probe" mission?

How would instruments aboard the "solar probe" detect solar wind particles, even though they are shielded from direct sunlight?

The solar probe near its closest approach to the Sun moves almost as fast as the solar wind, but in a direction perpendicular to that of the solar wind (which moves radially). In the probe's own frame of reference, therefore, solar wind ions move along slanting paths that brings them behind the heat shield.

The Theory of Relativity

What is the principle of relativity?

moving

at rest

How does the theory of relativity modify Newtonian mechanics?

Time does not flow at the same rate in the two frames. Two events which in one frame are a second apart, viewed from another frame may be two seconds apart.

muon

300,000 x 2/1000,000 = 0.6 kilometers

in its own frame of reference

distance

[Comment: After relativity was introduced, Newtonian mechanics also became known as "classical mechanics" to distinguish it from "relativistic mechanics." Later still different modifications to Newton's mechanics were found to be appropriate for atomic dimensions, and these became known as "quantum mechanics." (And in case you wonder: yes, there also exist "relativistic quantum mechanics")]

Lesson Plan #33 http://www.phy6.org/stargaze/Lflight.htm

#22c Airplane flight

In aviation it is usually more convenient to consider the motion of air over a wing or over a propeller blade in their own frames of reference. This lesson examines swept-back airliner wings (also at swept-forward and swiveled wings), and at the loss of propeller efficiency when the airplane gains forward speed.

This lesson plan supplements:
"Airplane Flight," section #22c http://www.phy6.org/stargaze/Sflight.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Note: This section is optional. Also, if time is short, the discussion of forces on a propeller (the more difficult part) may be omitted.

Goals

The student will learn:

Basic concepts about airplane flight.
The reason jetliner wings are swept back.
Why jet engines have replaced propellers in high-speed flight

Terms: frame of reference, relative velocity, lift, drag, thrust, angle of attack, wind tunnel, sweepback of wings.

Stories and side excursions: The wind tunnel of the Wright brothers, the swept-back wing, the X-29 airplane with swept-forward wings and the swivel-wing idea.

Starting the lesson:

Today we will discuss the application of frames of reference to an airplane flying with a constant velocity v through the air. Viewed in the frame of reference of the ground, in the absence of wind, the airplane is moving through still air.

If on the other hand we prefer to use the airplane as our frame of reference, then the air is what moves, blowing in the opposite direction to the flight and flowing around the wings and the aircraft.

We can look at it either way, but the second way is usually more convenient. In any case, it is the flow of air over the wings of an airplane that supports the airplane in the air, creating an upward force known as lift. Lift increases rapidly with velocity--as a matter of fact, it grows like the velocity squared--so with enough speed, even an airliner weighing 100-200 tons can be supported

We don't have the time here to discuss how lift is generated. Let it just be said, that the cross-section of the wing--flat on the bottom, curved on top--makes air flow faster over the top than over the bottom. This only happens when the front of the wing faces the wind (directly or lifted slightly, at a small "angle of attack").

When the airplane stands on the ground, not moving, air presses on the top and bottom of the wing with equal force. In flight, the faster flow on top of the wing creates lower pressure there, and the extra pressure from below is then what produces the lift.

Another force on the wing and on the airplanes is the drag--that is the name given to the air resistance, and it also grows like the square of the velocity. The drag is overcome by the thrust, the forward pull of the propeller or the push of the jet engine. And finally, the lift is opposed by the weight of the airplane and its cargo.

[As part of this discussion, it may help to draw on the board a side view of an airplane, and each time a force is mentioned, illustrate it by an appropriately directed and labeled arrow.]

Then continue from the text of section #22b, starting at the subhead "Frames of Reference."

Questions and side excursions

What are the 4 forces acting on an airplane in flight, and what are their directions?

Thrust of the engine

Drag

Lift

Weight

What creates the lift on an airplane wing?

The pattern of air flow over the top and bottom of the wing reduces the air pressure on the wing's top surface.

[Optional discussion:
Can the same lift force be applied to transportation by water?

Yes!

hydrofoils

Why do jetliners avoid flying above the speed of sound?

Because at supersonic speeds, air piles up in front of the aircraft and its wing, forming a compressed layer ("shock"), rather than smoothly flowing around the airplane. Compression heats up the air, and since heat is a form of energy, the process robs energy from the motion and greatly increases the drag force. It also reduces the lift of a wing, which depends on the orderly flow of air around it.

Why do jetliners avoid flying faster than even 85% of the speed of sound?

approaches

Why do swept-back wings allow an airliner to fly closer to the speed of sound?

along

across

However, a component of a velocity is always less than the full velocity. Therefore, in a swept-back wing the speed of the perpendicular flow will be smaller than that of the airplane. This allows the airplane to get closer to the speed of sound before shocks form on top of its wings.

Will wings swept forward have the same effect?

Yes, they will, as demonstrated on the X-29 airplane. However, the flexing of wings makes this design less stable.

Can the same advantage be obtained from a wing that turns around a swivel after the airplane has attained cruising speed--one wing is swept back, the other forward?

Yes it can, and such designs have been tested with models. The swivel-wing airplane can fly along a straight path, but cannot be safely steered.

Optional peripheral discussion--or riddle to ponder at home:

In the lobby of the Air and Space Museum in Washington hangs the "Voyager" airplane which flew non-stop around the world, taking more than a week. It took off at 138 miles-per-hour, using two engines, but it came back at only 78 miles per hour, with one engine turned off. Why the difference?

Flying nonstop around the world took a lot of fuel--in fact, fuel weighing many times more than the rest of the airplane. On take-off and in early stages of its flight, Voyager was heavily loaded, and to let its wings create enough lift to hold it aloft, it had to fly fast. Coming home, most of the fuel had been consumed, there was no need for such speed, and one engine could supply all the thrust that was needed.]

How does an aircraft propeller work?

Before take-off, when the airplane stands on the end of the runway and the pilot "revs up" the propeller, how does air flow in the frame of a propeller blade?

The air flows in a way similar to its flow over an airplane wing.

How does the above flow change when the airplane has appreciable forward speed?

If the propeller blade is viewed like the wing of a flying airplane, the added flow is like an added wind, blowing vertically downward. The combined flow appears to the blade like a head wind slanting downwards.

What is done to remedy this?

The blades of the propeller can be twisted (even in flight), in a way making them face the slanting flow of air.

What limits the usefulness of this remedy?

The lift force on the propeller is now at an angle. Only part of it pulls the airplane forward, the rest contributes a greater air resistance to the motion of the propeller. The faster the airplane flies, the smaller is the part that pulls and the greater the part that resists and must be overcome.

Lesson Plan #34 http://www.phy6.org/stargaze/Lframes2.htm

#23 Accelerating Frames of Reference: Inertial Forces

#23a Frames of Reference: The Centrifugal Force

Uniformly moving frames of reference experience no new forces. Uniformly accelerating frames and rotating frames do so. If we want to express the equations of motion in their coordinates, we must always add "inertial forces" to represent the effects of their acceleration. The centrifugal force is one such force, described here and illustrated by examples.

This lesson plan supplements:
"Accelerating Frames of Reference: Inertial Forces," section #23 http://www.phy6.org/stargaze/Sframes2.htm
"Frames of Reference: The Centrifugal Force," section #23a http://www.phy6.org/stargaze/Sframes3.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Note: This lesson uses vectors, and some way of denoting them on the board and in the notebook must be agreed on by the class. In this lesson plan, all vector quantities will be underlined.

Goals: The student will learn

That when applying the laws of motion in an accelerating frame to a body with mass m, using coordinates defined in such frame, one must always add an "inertial force" caused by the frame's acceleration..
In a uniformly accelerating frame, the inertial force opposes the acceleration. For instance, in a braking car (acceleration directed backward, opposed to velocity), the inertial force tends to push forward.
In a uniformly rotating frame, to the forces on a mass m must be added a "centrifugal force" mv²/r, directed away from the axis of rotation.
To clearly distinguish between the centripetal and centrifugal forces.
- The centripetal force is used when we calculate motion, using coordinates, velocities and accelerations of a non-rotating frame of reference.
- The centrifugal force is needed to describe the same motion, using coordinates, velocities and accelerations of a rotating frame of reference.
Examples of the inertial forces:
1. The force on objects inside a braking bus,
2. The centrifugal force on objects on the rotating Earth
3. The centrifugal force in a roller-coaster car going around a "loop the loop".

Terms: inertial force, accelerated frame of reference, rotating frame of reference, centrifugal force, bulge of the Earth.

Stories: Variation of g and the bulge of the Earth. (optional, at the end of this lesson plan: pumping a swing)

Starting the lesson:
Up to now we have dealt with uniformly moving frames of reference. That was easy: moving from one such frame to another, it was only necessary to re-define velocities and coordinates in terms appropriate to the new frame. The forces were the same, because forces, as Newton showed, depend only on acceleration.

Tody we go a step further, to accelerating frames of reference--in particular, two examples:

a bus whose driver suddenly hit the brakes, and
a rotating frame, say a bus turning a sharp corner.

From experience everyone knows what to expect. In the first case, the passengers are flung forward, in the second, they are pushed to the outside of the curve, by what is known as a centrifugal force.

Both these are a rather special type of force, called inertial forces: they only appear in the accelerating frame.

If we treat the motion in the coordinates of the accelerating frame--e.g. if your coordinates are those of the inside of the bus--they must be included.
If you solve the problem using the coordinates of an outer frame of reference, which does not accelerate or rotate--e.g. if your coordinates refer to position in the outside world--they do not exist.

For example: the bus which suddenly stops.

If we calculate position relative to the outside world, the situation is very simple. The bus is slowed down by its brakes, but the passengers keep going, until something--the seat belt, the seat in front--stops them.
If we calculate position relative to the bus, the passengers are pushed forward, to the seat in front, to the limits of the seat belt.

This can be quite confusing. Some teachers and textbooks avoid inertial forces altogether or call them "fictional forces". As we will see, however, they can be quite useful. One thing you should remember: be sure you know to which frame of reference your coordinates belong. With accelerated frames, all frames are not all equivalent.

***********

The best known example, of course, is a rotating frame of reference, where the centripetal force pushes inwards, and the centrifugal force pushes outwards. Which to use? Here is the rule: [on the board--all please copy]

centripetal

nonrotating

towards

The centrifugal force is only used in a rotating frame. It must be added to other forces in that frame, in order to take into account the frame's rotation, and is directed away from the axis of rotation.

As you will see, both describe the same physics, and either can be used to study motion. However, the centrifugal force seems more intuitive: this is what you feel when you sit in a car going around a sharp curve. You feel yourself pushed to the outside of the curve. Your mind is keyed to the frame of reference of the car that surrounds you, and in that frame you feel pushed outwards.

As a result, almost anyone knows intuitively what a centrifugal force is, while "centripetal force" is only familiar if you learned about it in school.

(Then continue with the material of section #23 in "Stargazers.")

Questions

An astronaut lies horizontally on a couch, flat on the back, inside a space shuttle as it takes off. In which direction is the astronaut accelerating?

--The acceleration is directed forward (=upwards, at least at first).

Does the astronaut feel pushed--and if so, which way?

down,

opposite

We agree the astronaut's body is pressed towards the couch. Viewed from the outside world, why that pressure?

Because the shuttle is accelerating, the couch is accelerating with it, and it in turn accelerates the astronaut's mass, through the pressure the couch exerts on it.

Viewed from inside the cabin, why that pressure?

If you have cartesian coordinates (x,y), what are the unit vectors x_u and y_u?

Vectors of unit length in the directions of the coordinate axes

What are unit vectors useful for?

Say you fire a gun at an angle upwards, so that

the initial upwards velocity is u, and
the initial horizontal velocity is w.

[draw it all on the board].
Let the direction of u be the y axis, and of w the x axis After t seconds, the upward velocity is (u-gt) while the horizontal one remains w. Express the velocity vector V after time t.

Is motion around a circle with constant speed ("uniform rotation") an accelerated motion?

Yes, it is.

Why is it accelerated, if the speed does not change?

direction

So, for a body with mass m to move with constant speed V around a circle of radius R, a force is needed. What is that force called, what is its magnitude and what is its direction?

It is called the centripetal force
Its magnitude is m V²/R
Its direction is towards the center of the circle.

You are standing on the floor, and your body is subject to two forces:

Your weight of F₁ newtons,
the reaction F₂ newtons of the floor, not letting you sink any further.

Your body is in equilibrium--it does not move. What can you say about those two forces?

₁

₂

[The discussion that follow may be helped by a crude drawing on the board].
You are sit on a whirling turntable, part of a carnival ride, at a distance r from the axis, going around at a velocity V. As before, F₁ is your weight and F₂ is the force exerted on you by the ride.
You hold tight and keep your position. If r_u is the unit vector pointing radially outwards from where you sit, which of these equations correctly describes your force balance?

F₁ + F₂ = (mV²/R) r_u
or F₁ + F₂ = -(mV²/R) r_u ?
The total force F₁ + F₂ on you--in the first case it is outwards, in the second inwards. Which is it?

₁

₂

Why?

Because...

into

towards

Another way of writing the same equation is F₁ + F₂ + (mV²/R) r_u = 0 How is this interpreted in the rotating frame?

You live on a rotating Earth. How does the centrifugal force affect you on the equator?

The force on your body is the sum of gravity and the centrifugal force. On the equator, the two are opposed, and therefore the effective value of g is slightly smaller there.

How does the centrifugal force affect you away from the equator?

It reduces the pull of gravity by a lesser amount than at the equator. In addition, it also slightly shifts the direction in which bodies fall, because while gravity is radial, the direction of the centrifugal force is parallel to the equatorial plane.

In which direction is the shift?

[sketch on the board the two forces and their head-to-tail vector addition: the gravity arrow goes down towards the center of the Earth, the centrifugal arrow continues from its end parallel to the equator.]

Falling bodies are slightly displaced towards the equator.

Does the centrifugal force of the Earth's rotation affect the Earth itself?

Yes, it, makes the earth oval instead of a perfect sphere. The equatorial radius of Earth is 6357 km, while the polar radius is 6378km (average radius, 6371 km)

Originally the meter was defined in terms of the distance from the equator to the pole, which was to be equal to 10,000,000 meters. If that were still the definition,would you expect the length of the equator to be 40,000 km? A little more? A little less?

Note:

Jupiter and Saturn both rotate around their axes in about 10 hours. Would you expect them to be more oval or more spherical than the Earth?

More oval; in fact, they look oval in the telescope. For Earth the difference between polar and equatorial radii is 1/297 of the radius; for Jupiter 1/15, for Saturn 1/9.5.

[Optional]
You are sitting on a rotating platform, right on the middle. You want one of the people sitting nearer to the edge of the platform to join you at the middle, so you extend your hand and pull that person in, against the centrifugal force.

What do you think: do you need energy to overcome the centrifugal force? Does your arm perform work?

did

There exists an interesting application. You are probably aware children can "pump up" a swing and keep it going; you may even have done so yourself. How is it done?

The process is best seen in swings on which you stand rather than sit. The centrifugal force on the swing varies: it is greatest at the bottom of the swing, where motion is fastest, but zero when the swing briefly stops at the end points. What you do is, near the end points you lower your body, then near the bottom of the swing you stand up straight again.

By standing up, you overcome the centrifugal force, which is directed towards your legs, so you invest energy. But energy is conserved and must go to somewhere else in the motion! It actually goes to the energy of the swinging motion, making the swing move more vigorously, or at least making it overcome the energy loss to friction, which would otherwise gradually slow it down.

The "pumping" of a swing by moving legs and body while sitting down is somewhat similar.

[Incidentally: the "Exploratorium" science museum in San Francisco had--and maybe still has--a swing which can be "pumped" by a rope which controls a weight on it. By pulling up the weight near the bottom of the swing and letting go near the end points, you can increase its swings and keep them going.]

Lesson Plan #35 http://www.phy6.org/stargaze/Lrotfram.htm

#24 Rotating Frames of Reference in Space and on Earth

This lesson continues to explore rotating frames of reference, focusing on the weightless environment in space and on a qualitative discussion of the Coriolis force.

This lesson plan supplements:
"Rotating Frames of Reference in Space and on Earth," section #24 http://www.phy6.org/stargaze/Srotfram.htm
"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Goals: The student will learn

Understand the "weightlessness" or "zero g" environment aboard spacecraft
Realize that weightlessness will occur in any frame of reference which moves freely, subject only to gravity (e.g. "freely falling").
Learn about the Coriolis force, another inertial force not covered previously. Like other inertial forces, it too appears only in a rotating (or otherwise accelerating) frame. While the centrifugal force acts on any object in the rotating frame, the Coriolis force only acts on objects that move in that frame, in a way that affects their distance from the rotation axis.

Terms: weightlessness (or zero-g), artificial gravity, Coriolis force.

Stories and extensions: The "Vomit Comet" airplane used by NASA to simulate weightlessness; "artificial gravity" in a rotating space station; the swirl of draining sinks and of storms, north and south of the equator

Starting the lesson:

This lesson continues the exploration of rotating frames of reference, in particular two of their features: weightlessness and the Coriolis force.

Every one here must have already heard of "weightlessness" in space, and has probably seen on TV astronauts floating weightlessly in the "zero g" environment of the space shuttle. It is not that the Earth's gravity does not extend to the shuttle's altitude--without gravity, how could it stay in its orbit?

So what is happening to gravity on the shuttle? To get a better understanding, let us look at a few examples of gravity in action:

Example 1: When you jump down from a truck or a wall, gravity pulls your body down and gives it an acceleration g--until your feet are stopped by the ground.

Example 2: When you stand on the floor, gravity also pulls your body down. But you do not move and do not accelerate, because the floor won't let you. It produces an opposing force which prevents any motion, and your body is now in an equilibrium.

In example 1, gravity is the only force present, and you accelerate. In example 2, two opposing forces cancel each other, and nothing moves.

Now, Example 3: You watch on TV an astronaut inside the orbiting shuttle, standing in front of the camera. The way gravity acts on that astronaut's body--which of the preceding two examples does it resemble? The person jumping from a truck, or the one standing on the floor?

[The class may discuss the question briefly.]

It sure looks like example 2, the person standing on the floor. But actually it is much closer to example 1, the jump from the truck.

Once again: In example 2, two opposing forces cancel each other, and nothing moves.

In example 1, gravity is the only force present, and your body is accelerating.

The astronaut in front of the camera is moving, at the orbital velocity of 8 km/sec.
The astronaut is accelerating, because motion in a circular orbit (or in any non-straight orbit!) is accelerated. And
Gravity is the only force present.

The only reason motion is not evident is that the shuttle and camera are also moving and accelerating, just as fast. Gravity is already fully employed, it is producing all the acceleration it can, and there remains no additional force that would push the astronaut against the floor. So to the person in space, this feels like weightlessness.

If the orbit is an exact circle, gravity supplies the centripetal force needed to maintain it, so we have....
***********************
[continue with the first equation in section #24, up to "The Coriolis Force" which is introduced below.]
***********************

The second half of this unit is concerned with the Coriolis force.

The centrifugal force, you will recall, is an inertial force--one which only enters the calculation if the motion is described in a rotating frame of reference. In that frame, if the centrifugal force on some body is balanced by some other force, that body is at rest.

If however the body is is moving in the rotating frame, and we want to use its equations of motion in the rotating coordinates, we not only need to add the centrifugal force, but may also need another inertial force--the Coriolis force. Unlike the centrifugal force, it only comes into play when an object moves in the rotating frame, in such a way that it changes its distance from the rotation axis.

[The discussion that follows can use a sketch on the board.]

At any point in a rotating system, you move around the axis with a certain velocity. The greater your distance from the axis, the greater the velocity. And when you move in the rotating frame to a greater and smaller distance from the axis, your velocity should also increase or decrease. Wouldn't you think that inertia would resist such changes? It does--and that is the essence of the Coriolis force.

A good example is given by a rotating space station, the kind that was first proposed in the early 1950s. It was then suggested that the centrifugal force might provide an "artificial gravity" in space, inside a wheel-shaped rotating space station...

[Continue in section #24, from the heading "The Coriolis Force"]

Questions

Are astronauts weightless in space because they have gone beyond the reach of Earth's gravity?

No. Even as far as the Moon, Earth's gravity is still felt, since that is what keeps the Moon in its orbit.

If astronauts are not free from the Earth's gravity, why do they feel weightless in orbit?

In a high dive into a pool of water, in the time between leaving the diving board and entering the water, is the diver weightless?

Essentially, yes (air resistance interferes--but more so with skydivers). That is one reason why divers can perform intricate twists and somersaults. .

One of the rides in the "Great America" amusement park in Santa Clara, California, is the "Drop Zone" (other parks have similar rides), centered on a 220-foot tower with vertical rails running down its side. Riding on each rail is a frame holding several seats. At the foot of the tower, riders are strapped into those seats and and then the frame is pulled up to the top of the tower.

At the appropriate moment, the frame is released and plunges down, in what is essentially a free fall. At 1/3 of the tower's height, brakes become active and break the fall, so that by the time the ground is reached, all the falling speed is again lost. How many gravities do the riders feel (1) in the free-fall phase, (2) in the braking phase (assuming a constant rate (-a) of deceleration)?

(2) Suppose the tower's height is 3h: the riders fall a distance 2h with acceleration g, then stop within distance h with acceleration -a (here a negative number). You would guess the riders would have to decelerate twice as fast

a = 2g

producing on them an additional inertial force 2mg. That, however, is in addition to their own weight mg, making the total force 3mg, or 3 gravities.

[ Optional] That guess is correct and here is a formal calculation: Suppose V is the velocity achieved at the end of the free fall. From conservation of energy

2hmg = mV²/2 hence V² = 4hg

The formulas for accelerated motion are like the ones for free fall, but with the acceleration (-a) in place of g. Suppose the braking motion takes a time t. Then

v_final = v_starting - at or 0 = V - at

_starting

A space payload must achieve 8 km/sec to go into orbit. Can NASA get a "head start" on that motion by launching in the direction of the Earth's rotation? Is this equivalent to starting out with a velocity equal to the velocity of rotation at the Earth's surface, about 400 meter/sec near the equator? If not--why not?

does

A large low pressure area in the northern hemisphere has air flowing into it and swirling (as was seen in the lesson) counterclockwise. Suppose instead we have a high pressure area, with air flowing out. Will it swirl? And if so, in what direction? Give reasons.

cyclones

anticyclones

Lesson Plan #36 http://www.phy6.org/stargaze/Lsun1lit.htm

(S-1) Sunlight and the Earth

A discussion of the solar heating of the Earth and atmosphere, its heat loss processes, and the way these relate to weather and climate.

This lesson plan supplements: (S-1) Sunlight and the Earth http://www.phy6.org/stargaze/Sunlite1.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Note to the teacher: This first unit in a sequence on the Sun actually deals with solar heating of the Earth, and is also suitable for a course on weather and climate. It acquaints the student with concepts of heat radiation and convection.
Originally the lesson plan included many additional aspects of the weather, later moved to a separate section, Weather and Climate. The teacher may include them if more extensive coverage of these topics is needed.

Goals: The student will learn

The student will learn

How the Sun supplies almost all the energy we use.
About radiation emitted by hot objects ("black body radiation").
About the balance between incoming solar energy and outgoing heat, radiated by Earth back into space.
About the "greenhouse effect" and gases that contribute to it.
That convection of heat in the atmosphere is the cause of weather phenomena.
That water vapor also carries solar heat and plays an important role in atmospheric convection.

Terms: radiation (visible, infra-red, ultra-violet), radiation balance, greenhouse effect, greenhouse gases, ozone, convection, thermal currents, buoyancy, stratosphere, troposphere, (humidity)

Starting the lesson:

Today we start our discussions of the Sun, by first looking at the effect Sun has on our environment on Earth. Almost all the energy used by people on Earth comes from the Sun. Can anyone give an example?

Food grown by crops exposed to sunlight, or obtained from animals which eat such crops.
Solar cells that power satellites, calculators etc.
Solar water heaters on rooftops.
Cars use gasoline or other liquid fuels that originate from fossil plants.
Electricity may be generated by coal--from fossil plants, too.
Windmills are powered by winds, whose motion is caused by solar heat as discussed later. (Ocean wave energy also comes from winds.)
Hydro-electric power comes from water descending from mountains: it was lifted into rain clouds by the Sun's heat.
In addition, all the water we drink is distilled by sunlight. Were it not for the Sun, all water would be salty.
Sunlight dries laundry strung on a line.
In some countries, sunlight is used to produce salt from sea-water (in ponds) and to dry tomatoes, figs, fish etc.

Do you have an example of energy not from the Sun? (may be skipped if time is short)

Nuclear power, from splitting up the nuclei of heavy atoms, as will be discussed in section S-8.
Nuclei carry a net positive electric charge, because of the positive protons which they contain. A heavy nucleus of uranium or plutonium can be made to split into two parts, each positively charged, and because the fragments strongly repel each other, each gains a lot of speed and energy. As the fragments collide with matter around them, their energy becomes heat, that heat is used to create high-pressure steam, which turns turbines turning electric generators. (Teacher draws diagram on the board: fission in reactor becomes heat in a boiler, which turns turbines to generate electricity.)
Geothermal heat, e.g. the heat of volcanoes, geysers and hot springs, on land and on the ocean floor. In some places (e.g. Iceland) geothermal steam is used to produce electricity. This energy comes from radioactivity. The Earth contains a small amount of radioactive uranium and thorium (and radioactive substances created by them, "daughter products"), as well as radioactive potassium. All these emit fast particles which heat up the surrounding material. This is a slow process, governed by chance, and the probability of any atom of the above substances undergoing "radioactive decay" in a given year is less than one in a billion.
However, even a weak heating process can create high temperatures, if the heat has difficulty escaping.
You can think of an area of 1 meter² in the ground on which you stand as the top of a deep wedge running all the way to the center of the Earth. On the average, the heat produced by radioactivity in that wedge must escape through that same area. So much volume, so little surface! That is why the Earth deep down has a temperature of thousands of degrees, able to melt lavas and produce volcanos.
The tides, raised by the pull of the Sun and the Moon. In principle, tidal energy could be exploited, except that technically it is very difficult to run turbines on small differences of height.
(Someone may mention starlight: yes, in principle...)

Then go into the lesson. Questions about the material:

How is the temperature of the Sun related to sunlight?

The Sun radiates because it is hot. All hot objects radiate, though sometimes the radiation is outside the range of the human eye.

What does sunlight tell about the Sun's temperature?

Judging by its color distribution, the emitting layer of the Sun has an absolute temperature of about 5780° (degrees centigrade from the "absolute zero" of -273.1° centigrade, at which all heat motions cease). The Sun's surface temperature will be again discussed in a later lesson.

What does this say about the surface of the Sun?

The material on the surface of the Sun cannot be solid or liquid, because at 5780⁰ all known substances are vaporized. In fact, some will be ionized, with at least one electrons ripped off and floating independently nearby.

The top layer of the Sun, from which sunlight comes, is known as the Sun's photosphere. All words that start with "photo" are related to light. Know any?

Photography and words derived from it--photoelectric flash, photogenic, photostat (picture) etc.
Also photosynthesis, photo-electric cell (or "photo-electric eye"; also "phototube"), photon ("particle" of light--see later lesson; also "photon torpedo" in "Star Trek"), phot (unit of light, favorite in crossword puzzles), photolysis (chemical dissociation caused by light) etc.

If the Sun constantly heats the Earth, how come the Earth does not heat up?

The Earth also radiates back into space, emitting infra-red light (IR) which our eyes cannot see. On the average, the energy the Earth receives is balanced by the energy it loses.

How can the Earth radiate back as much as it receives from the Sun, if its absolute temperature is only around 300⁰, while that of the Sun is 5780⁰?

Take an area A on the surface of the Earth. It receives "hot" sunlight only from a small patch of the sky, about 0.5⁰ across, but it radiates back infra-red (IR) to half the sky. Clearly, if incoming and outgoing energy flows are to be equal, it does not have to shine anywhere as brightly as the Sun!

(optional discussion)

You probably know that with a magnifying glass you can use sunlight to create a lot of heat--enough even to start a fire. Why?

(Someone may say "because it concentrates the Sun's light.")
Correct. Is there a limit to the temperature you can get?
Someone may say "no" because all the light seems to converge to a point.
Actually, you cannot get a greater temperature than that of the surface of the Sun. Here is why.

Suppose you use a magnifying glass to set a piece of paper on fire. Viewed from the point on which the sunlight is focused, the Sun is magnified--no longer 0.5⁰ across but maybe 3⁰, 5⁰ or 10⁰. Its heating power is then magnified by the square of the ratio between the angles--36, 100 or 400 times, because the heat the paper receives goes like the area of the bright patch which shines on it.

There exist solar furnaces with arrays of mirrors that can magnify the Sun even more, so that viewed from the focus, it covers (for instance) 1/10 of the sky. The heat generated may be intense enough to melt iron. However, as the object at the focus heats up, it also radiates away more heat!

Suppose that by some clever arrangement of lenses and mirrors we have managed to illuminate the object at the focus from all directions. Whichever way it "looks" it sees the Sun. At equilibrium, the heat it gets equals the heat it radiates back. How hot does it get?

Suppose it is hotter than the Sun. If brightness depends only on temperature (very nearly true), then it is also brighter than the Sun, and in any direction it radiates back to the Sun more than it receives. That is obviously impossible, so we conclude that the sample can never exceed the temperature of the photosphere which provides its light in the first place.

(end of optional section)

So far we have assumed the Earth receives visible light radiated by the Sun and radiates it back into space as infra-red light, less concentrated but in all directions.

Actually this assumption is more appropriate for the Moon or for the planet Mercury. It is not quite accurate for Earth. Why?

(someone may say "because the Earth has an atmosphere")
Correct. But why does the atmosphere make a difference?
Two reasons:

Clouds reflect heat before it reaches the ground
Air absorbs infra-red light

Correct. One can understand the effect of clouds.
But with the atmosphere--isn't any energy absorbed by the atmosphere radiated out again--or else, the atmosphere would get hotter and hotter? Yes, it is. Anything absorbed by the atmosphere is radiated away again. But some of it is radiated downwards and returns to Earth! Therefore the existence of the atmosphere impedes the outflow of heat.

Why is this process called "The Greenhouse Effect? "

Because the same process keeps glass-covered greenhouses warm. The Sun heats the ground and greenery inside the greenhouse, but the glass absorbs the re-radiated infra-red and returns some of it to the inside.

What substances in the atmosphere contribute to the "greenhouse effect"?

The ones that absorb IR light. Water vapor (H₂0) is important, so is carbon dioxide (CO₂) produced by burning fuel, still another is methane (CH₄) emitted by decaying vegetation and also by the digestion process in cows and related animals.
The concentration of CO₂ in the atmosphere has increased significantly in the last century, because of the burning of coal and other fossil fuels. This might be responsible for the warming trend in the world's climate observed in recent decades.

What is ozone?

Ozone is a form of oxygen, forming the molecule O₃ instead of the usual O₂. It forms in two places: high in the atmosphere, between 18 and 50 km (peak at 25) where it is beneficial in absorbing ultra-violet light, and near the ground, part of urban air polution. Ozone is very reactive chemically, so near the ground it erodes paint and is unhealthy to breathe.

Is ozone a greenhouse gas?

Yes, it is one, too. It is true it also prevents solar UV from reaching the ground, and that reduces the heating of the ground: but it is a very slight effect, because UV does not carry much energy. Of greater concern are the harmful effects of increased UV on the skin and eyes.
However, ozone also absorbs infra-red light. As far as the heat balance is concerned, this effect is more important. Overall, therefore, the presence of ozone helps keep the Earth warm.

What other processes affect the heating and cooling of the Earth, besides absorption and emission of light and of radiations like IR and UV?

Someone may say "heat generated by human activities":

Big cities are indeed slightly warmer, but overall the heat released by human activities is too small to have any great effect.
Someone may say "weather":
Well--yes. But what are the two things that characterize weather besides the temperature of the air?

Wind
Rain

So let's talk about wind, and then about rain--or to use more technical terms

The flow of air
The evaporation and precipitation of water

Why does warm air rise?

Warm air is less dense than cold air, and therefore floats up (the way oil that is less dense floats on top of water).

How does a hot-air balloon work?

A burner heats the air that fills the balloon: it is lighter than the air around it and rises.

What does rising air have to do with the warming of the Earth by the Sun?

It is one way the ground removes heat: it warms up the air near it, which rises. Later, higher up in the atmosphere, the air radiates its heat out to space, cools down and gets denser, then sinks down again, replaced by warm air that is still rising. This is known as the convection of heat.

How is heat convected near a cold window? How does air flow there?

It flows downwards. Air touching the window cools, gets heavier and drops to the floor. It then spreads into the house where (if the house is heated) it is warmed up again. Meanwhile other air is replacing it near the window and is getting cooled in its turn.

(Note: Fiberglass is a good heat insulator, because it prevents the air inside it from flowing. As long as the air does not move, it does not carry away much heat. Wool blankets and sweaters work the same way.)

Convection in the atmosphere stops around 10-15 kilometers. What is the layer above that called, and what do you know about it?

It is called the stratosphere and is pretty stable and cold (though its higher layers get heated by ultra-violet, absorbed by ozone.) The region below it--where weather is found--is the troposphere, and the boundary between the two is the tropopause.

(If you have seen an isolated thunderstorm from a distance, you might have noted that its top is flattened and spread out. It is flattened against the bottom of the stratosphere, which blocks the convection of the storm from rising any further.)

What role does water play in moving the Sun's heat outwards?

Part of the energy of sunlight goes to heating the ground, but another part evaporates water, from the oceans, lakes, rivers and plants.
As warm humid air rises, it carries energy in two forms--some as heat, some as humidity.

What causes rain?

As warm air rises, it expands and cools. Cold air cannot hold as much water and some is forced out, creating clouds and rain.

On a summer morning you get up and find the grass outside covered with dew--with drops of water. How did they get wet?

The ground cooled down during the night, and cooled the air. The cooled-down air had to give up some water, and deposited it on the grass.

When humid air gives up water as rain, does it speed up its cooling or slow it down?

Slow it down. When sunlight evaporated that water, it invested energy in the process. But energy in nature is always conserved! When the water is forced out, that energy is returned to the air, adding to its heat.

Lesson Plan #37 http://www.phy6.org/stargaze/Lsun2vue.htm

(S-2) Our View of the Sun

An introduction to solar observations--by eye or telescope (with cautions) and during eclipse. Also, the distance of the Sun, its layers, the corona and the solar wind.

This lesson plan supplements: (S-2) Our View of the Sun http://www.phy6.org/stargaze/Sun2view.htm

"From Stargazers to Starships" home page: ....stargaze/Sintro.htm
Lesson plan home page and index: ....stargaze/Lintro.htm

Goals: The student will learn

Safety rules for observing the Sun
How the distance of the Sun, about 150,000,000 km, must be measured indirectly, using Kepler's laws.
About the visible layers of the Sun--photosphere, chromosphere, corona.
About the high temperature of the corona, the evidence for it and what makes it so puzzling.
About the solar wind and its connection to the Sun's corona.

Terms: astronomical unit, plasma, photosphere, chromosphere, corona, solar wind.

Start the lesson by discussing a solar eclipse:

Who here has seen an eclipse of the Sun? Total? Partial? Actual observations, or over TV?
How does one observe an eclipse? What should be avoided? What may one do?

any

do not

completely

Looking directly can be harmful--and you will be too dazzled to see any details. Looking through binoculars or through a telescope is very dangerous--as if you focused a magnifying glass onto your eye! On the other hand, once the Sun is completely covered (in a total eclipse only), it is safe to look and to photograph.)

What can one see during a total eclipse that is not visible otherwise?

The chromosphere, a reddish ring around the Sun.
--The corona with streamers extending above active sunspots,
"Plumes" above the poles and arches above sunspot groups, both these suggesting magnetic fields.

Students who observe a total eclipse should be cautioned, however, not to expect to see all the fine details one finds in eclipse photographs. Pictures that appear in journals often use time exposures and superpositions to make the outer fringes of the corona appear brighter than they actually are. For instance, a picture shown on the web of the total eclipse of 11 August 1999 was actually obtained by blending more than 20 pictures.

Additional points the teacher may raise:

Total solar eclipses were once used to look for an additional planet orbiting very close to the Sun. Because of the glare of the Sun, such a planet would be invisible at any other time. Astronomers had even proposed a name for is--Vulcan. No such planet was ever seen, and astronomers today agree that none exists.
In the early 1800s, the German amateur Heinrich Schwabe, using a telescope (with a projected or filtered image) watched the Sun day after day for years, trying to see Vulcan passing in front of the disk of the Sun, when it should be visible as a dark spot (click here for a picture of the planet Mercury in front of the Sun). To distinguish such spots from sunspots, Schwabe carefully noted down all the sunspots he saw. He never found a planet, but after about 17 years, in 1843, he discovered the 11-year cyclical rise and fall in the number of sunspots, which had eluded professional astronomers.

A recent discovery (14 Nov'99): As discussed in connection with Kepler's first law, planets orbit not around their central star but around the common center of gravity of their planetary system (see here). The central star also orbits that point, and this causes its position in the sky to wobble slightly. Astronomers have used such wobbles--or more accurately, the changes of speed associated with them, which slightly shift spectral colors--to detect the existence of planets around more than 20 stars.

Most of those planets are as big as Jupiter or bigger, because obviously the heaviest planets shift the center of gravity by the greatest amount (the effect of an Earth-size planet is still too small to be measured). Many of them were detected by Paul Butler (Carnegie Inst.), Geoffrey Marcy (U. Cal Berkeley) and Steve Vogt (U. Cal Santa Cruz), who worked out a sensitive method for such observations.

The observations do not tell much about how the orbit is oriented in space, but for one recently discovered planet we now know a bit more. It orbits a star catalogued as HD 209458, some 153 light years from Earth, and happens to pass right between us and it. The researchers were hoping to find such a planet, and sure enough, Greg Henry of Tennesse State Univ, using an Arizona telescope, detected on November 7, 1999 a temporary drop in the light intensity by 1.7%. It is a big planet with about 2/3 the mass of Jupiter, and its orbital period is about 3.5 days. Because it orbits very close, and its size is expanded by the heat of its nearby star, it is considerably larger than Jupiter, able to block a measurable amount of starlight.

A total solar eclipse was also used in 1919 by the British astronomer Arthur Eddington to check out the general theory of relativity of Albert Einstein. Einstein predicted that the Sun's gravity would bend starlight passing close to the Sun. If that happened, stars whose position in the sky during a total eclipse was close to that of the Sun should have been very slightly shifted from their usual positions. The effect was very small, but Eddington confirmed its existence.

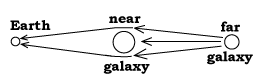
Today we know a handful of cases in which a very distant galaxy is obscured by a nearer one. You might think that the distant galaxy would be invisible, hiding (so to speak) behind the nearer one. However, the gravity of the nearer galaxy can bend light from the distant one, light which otherwise would have missed Earth, so that it does reach us. If the positioning is right, we see multiple images of the obscured galaxy. That phenomenon is known as gravitational lensing.

(end of additional material)

Chromosphere, corona--does the Sun have any other visible layers?

photosphere,

Teacher's explanation of the heat outflow of the Sun:

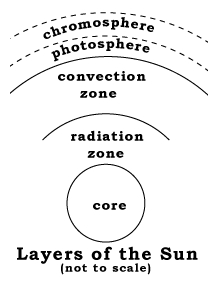The heat of the Sun is generated deep inside, in the Sun's core, by processes which require very high temperatures and great pressure (these will be studied in a later lesson).

That heat moves outwards from the core, towards the Sun's surface, by processes somewhat like the ones by which heat works its way through the atmosphere, from the surface of the Earth to space (section S-1).

No one of course can observe what happens deep inside the Sun, but a theory has been developed about the interior of stars, suggesting heat in the deepest layers travels by radiation. Atoms radiate light and neighboring atoms absorb it, but since the deep layers are compressed with atoms packed close to each other, the process is more like the conduction of heat. As heat moves outwards, the temperature keeps dropping, because net flow of heat can only take place from hot material to colder one.

Closer to the Sun's surface, the theory predicts, heat is carried by convection, as in the Earth's atmosphere--by gas flowing around closed paths. All these layers are still fairly dense, and any light emitted is quickly absorbed again. The photosphere is the final layer. Not enough material remains above it, allowing any light emitted there to spread out into space. It is a relatively thin layer, of the order of 100-200 kilometers

Because most sunlight comes from the photosphere, the much fainter chromosphere and corona are only seen during a total eclipse, when the light of the photosphere is completely blocked by the disk of the Moon.

However, astronomers can also view the Sun through special filters which reject all of the Sun's light except one or another narrow range of color ("spectral line," discussed in a later lesson). In some such colors, the chromosphere or the inner corona shine brightly enough to be seen even without a total eclipse.

How thick is the chromosphere?

About 5000 kilometers.

How does this thickness compare to the radius of the Sun?

It is less than 1% of the Sun's radius, which is about 700,000 kilometers.

How does the radius of the Sun compare to that of Earth?

It is more than 100 times bigger.

What are the approximate temperatures of the chromosphere and Corona, in degrees centigrade?

About 50,000° and 1,000,000°.

Why is that so puzzling?

Because the only credible source of the heat is the Sun itself. However, heat always flows from a hot temperature to a lower one--never the other way around. The photosphere below these layers is cooler: how then can it heat the chromosphere and corona?

How can we be sure that the corona is so hot?

The light from the corona is characteristic of atoms which have lost quite a few electrons (more about that, in a later lesson). At the density of the corona, this requires collisions between fast atoms, and the speed of the atoms of a gas is directly related to its temperatures.

So, what can be the explanation of the heat of the corona?

The energy must arrive at the corona in a form different from heat--perhaps as sound-like waves, or as a population of fast ions produced by such waves.

Any older explanations?

At one time it was proposed that a steady flow of small meteorites was hitting the Sun. However, nothing like them was ever observed passing near Earth.

What is the solar wind?

A fast flow of ions, streaming out from the Sun in all directions.

What produces the solar wind?

Its energy comes from the heat of the corona. Its top layers are so hot that they manage to escape the Sun's gravity.
[If the corona were like the Earth's atmosphere, its temperature would gradually drop with height. However, the corona is hot enough to be a plasma, a mixture of free-floating positive ions and negative electrons. Plasmas conduct heat well, and this does not allow the high layers to stay cool.]

How fast does the solar wind move, what is its density at the Earth's orbit, and what is it made up of?

Its velocity is about 400 km/sec, density at the Earth's orbit about 6 ions/cm³ , both these varying widely (at a distance of r astronomical units, the average density becomes 6/r²). Its composition resembles that of the Sun--mostly ionized hydrogen (protons), some helium and a small amount of heavier elements.

A calculation on the board

A proton's mass is 1.67 10^-27 kg. Assuming the solar wind consists entirely of protons, how much mass does the Sun lose each second? Assume the mean Sun-Earth distance ("astronomical unit") is 150,000,000 km.

(This calculation tests ability to use scientific notation when working with very large and very small numbers. The teacher might call up a student to derive it on the board, with the class copying).

1 AU = 150,000,000 km = 1.5 10⁸ km = 1.5 10¹¹ meter = 1.5 10¹³ cm

The area of a sphere with radius r = 1 AU around the Sun is

4pr² = (12.56) x (2.25 10²⁶) cm² = 2.826 10²⁷ cm²

Imagine behind every square centimeter a column of solar wind 400 kilometers long, waiting to cross it during the next second! (Teacher could illustrate this with a sketch on the board).

The entire surface of the sphere is therefore crossed each second by the solar wind particles contained in a volume

(2.826 10²⁷ cm²) x (4 10⁷ cm) = 1.13 10³⁵cm³

And with a density of 6 ions/cc, the number of ions is

(1.13 10³⁵) x 6 = 6.78 10³⁵

The total mass lost by the Sun each second is

(6.78 10³⁵) x (1.67 10^-27 kg) = 1.13 10⁹ kg = 1.13 10⁶ ton

The Sun therefore loses about a million tons each second. It sounds like a lot but really isn't--one cubic kilometer of the ocean contains about 1000 times more, and the Sun is not much diminished even if this loss continues for many billions of years.

(end of calculation)

What ultimately happens to the solar wind?

It gets lost in interstellar space. Actually, a boundary is expected, the "heliopause" marking the outer limit of the solar wind domination, from where on the interstellar gas determines the ambient conditions. The space probe "Voyager 2" is going to reach it, but whether it will still be transmitting remains to be seen.

Lesson Plan #38 http://www.phy6.org/Stargaze/Lsun3mag.htm

(S-3) The Magnetic Sun

An overview of phenomena related to the magnetism of the Sun, in particular to sunspots and their 11-year cycle, solar flares and magnetic disturbances at Earth caused by "solar activity." Also reviews briefly the connection between electricity and magnetism

This lesson plan supplements: "The Magnetic Sun," section #S-3
http://www.phy6.org/stargaze/Sun5wave.htm

"From Stargazers to Starships" home page and index:
http://www.phy6.org/stargaze/Sintro.htm

Goals: The student will learn here

That magnetic forces in nature rarely involve iron, but are actually forces between electric currents.
About sunspots and their intense magnetism, with a strength of about 0.15 Tesla (1500 gauss).
About the 11-year sunspot cycle and its discovery.
About "solar activity" associated with sunspots and their cycles, e.g. the abrupt brightenings known as solar flares.
That solar activity is probably associated with the release of magnetic energy, and that such releases can propel fast plasma flows towards Earth, causing there "magnetic storms."

Terms: Sunspot, magnetic field lines, magnetic fields, sunspot cycle, solar activity, solar flare, magnetic storm, magnetic energy

Stories: The discovery of electromagnetism by Oersted and Ampere, the discovery of the sunspot cycle by Heinrich Schwabe and the discovery of solar flares by Richard Carrington.

The teacher is advised to read those stories ahead the class, to be better able to present them to students, including the original articles, here and here. (Students can also be assigned to do so and to make the presentations.)

Starting the lesson:

(As described here, the teacher would begin the lesson around the above stories of discovery)

No area of science draws as much interest as stories of discovery, and of the unusual people who made them. This class has already covered some interesting discoveries. Which of them were associated with the names of... Aristarchus? Erathostenes? Columbus (even if it wasn't a scientific discovery)? Copernicus? Kepler? Newton?

Louis Pasteur was a French biochemist in the 19th century, whose many discoveries included a way of preserving food by heating ("pasteurization") and a procedure for saving the lives of people bitten by animals infected with rabies, which up till then meant almost certain death. Commenting on scientific discoveries, Pasteur said "chance favors the prepared mind". Discoveries often depend on luck--but luck is not enough, the mind must be prepared to exploit its opportunity.

[a student might prepare a poster with that quote, to hang in class]

Today as we discuss magnetism and magnetic phenomena on the Sun, we will discuss three discoveries in which luck had a part--but luck wasn't the only reason. (List on the board--students copy.)

The discovery of electromagnetism in 1820 by Hans Christian Oersted, in Denmark, and its explanation by Andre-Marie Ampere, in France.
The discovery of the sunspot cycle (1843, widely accepted around 1851) by Heinrich Schwabe in Germany.
The discovery of solar flares (1859) by Richard Carrington in England

(possible comment: Each discovery occured in a different country!. Science is truly international.)

The discovery of the connection between electricity and magnetism

What do we know about magnetism of iron magnets?

Like poles repel, unlike poles attract.
The magnetic compass tends to point north-south.

[Why is plain iron attracted to a magnet? Because when iron is in the region of influence of a magnet--its "magnetic field"--it becomes temporarily magnetic itself, with the pole closest to a pole of the magnet having opposite polarity, causing it to be attracted.]

What magnetic phenomena do not involve iron, and why are they called "electromagnetic" phenomena?

The attraction between parallel currents in the same direction, and the repulsion between them if the currents flow in opposite directions.
The forces between the coils, etc. used in electric machinery all follow from this basic property.

(optional)

The magnetic field which satellites observe in space is often different from what one would expect, based on the fields we observe on the ground.

The reason is that large electric currents often flow through the space surrounding the Earth, and they contribute their own magnetic fields as well. The currents can flow there, because of the presence of free electrons and ions (a "plasma").

What to you think--would such currents tend to spread out to cover as much space as possible, or would they narrow down to string-like filaments? You must give a reason.

[If no one answers:"It has to do with the forces between electric currents."]

They might tend to narrow down. A current flowing along a wide tube may be viewed as composed of many narrower parallel currents, and we know that parallel currents attract each other.

(This tendency of currents to narrow down has also been observed in laboratory plasmas, where it is named the "pinch effect.")
(end of optional part)

Suppose you had a compass needle able to point in any direction in space, not just horizontally. How would the northward-pointing end of the needle point at

The northern magnetic pole
The southern magnetic pole
Halfway between
Elsewhere?

[Note: such needles are available--see end of section S-3, or click here: http://www.cochranes.co.uk/BNRVP30/edu5.htm]

Straight down at the north magnetic pole, straight up at the southern pole, horizontally northward at the magnetic equator, northward slanting down in the northern hemisphere, northward slanting up in the southern hemisphere.
(By the way: the early Chinese who discovered the magnetic compass claimed it pointed south.)

How would such a needle point near a straight wire carrying an electric current? (Neglect the Earth's magnetism)

Perpendicular to the current.

How was the connection between electric currents and magnetic force discovered? (Students tell about it, or else, the teacher.)

What are magnetic field lines? Base your definition on the magnetic needle described above.

They are imaginary lines giving at each point the direction in which our 3-D needle would point, if placed there.

What are magnetic field lines used for?

They were originally used to graphically describe magnetic fields. In the rarefied plasmas of space, however, they also guide the flow of particles and currents. This is why arching solar formations above magnetic sunspots sometimes resemble the field lines of bar magnets.
(The guiding property of field lines also makes possible the trapping around Earth of ions and electrons in the Earth's radiation belts. The motion of these particles stops and reverses before they hit the Earth, because they are also reflected from regions of stronger magnetic field, found closer to Earth.)

What is Andre-Marie Ampere remembered for?

He explained the observations which baffled Oersted, and in doing so gave the first clear idea of what magnetism was. In his honor the unit of magnetic current is called the "Ampere."

[P.S.: He is also remembered as the man who was invited to dinner with Napoleon and forgot to go!]

The intensity of the Earth's magnetic field at the magnetic equator is about 31,000 nT (nanotesla) or 0.31 gauss. The field intensity goes down with distance r like 1/r³. If the intensity of the interplanetary magnetic field at the Earth's orbit is 5 nT (a typical value), at what distance--in Earth radii--is this matched by the Earth's field? (Needs calculator capable of extracting cube roots.)

If at a distance of 1 Earth radius the field is 31,000 nT, at distance of r earth radii is is 31,000/r³ . If r is the distance where it drops to 5 nT, we get 31,000/r³ = 5 . Multiply both sides by r³, divide by 5 to get

r³ = 31000/5 = 6200 r = 18.4 Earth radii.

Then go on to the discovery of sunspots.

When and how were sunspots discovered?

In 1609, when telescopes were first used in astronomy. Galileo, Fabricius and Scheiner all claim credit and might be independent discoverers.

What did the discoverers see?

They saw dark spots on the Sun.

How do we know that the Sun rotates around its axis?

Sunspots were observed to travel across the face of the Sun in a way that suggests they rotated with it.

What is unusual about the Sun's rotation?

The rotation period depends on latitude: the equator rotates fastest, in about 27 days. Nearer to the pole it can be 2.5 days longer.

Optional: The teacher may draw a table with the observed latitude dependence of the rotation period (in days) and let students graph it:

Solar Latitude	Actual Period	Period Viewed from Earth
0	25.03	26.87