|
Goals: The student will learn
Terms: uniform circular motion, frequency, peripheral velocity, centripetal acceleration and force.
Starting out: Today we will learn about the simplest case of motion not in a straight line, uniform motion around a circle. Of course, that is an accelerated motion, because by Newton's first law (or at least, by what that law implies), any motion not in a straight line is accelerated, and requires a force for maintaining it.
The string does not allow it to do so, but pulls it back towards your hand, to keep it in its circle. We will show today that motion in a circle can be viewed as the combination of two motions taking place at the same time--like the motion of the airplane, flying in a cross-wind (Section #14).
The other is a motion towards the center of the circle (draw it, too), returning the weight to its circular path. (Figuratively returning it; in actuality, both motions are simultaneous and the weight never leaves the circle.) That second motion, it will be shown, is an accelerated one... Now for the details..... (Continue on the board with the derivations, while the students copy into their notebooks.)
Guiding questions and additional tidbits (Suggested answers, brackets for comments by the teacher or "optional")
--Why is motion at a constant speed around a circle an accelerated motion?
--When you whirl a stone at the end of a string and let go, how does the stone move?
-- Why doesn't the released stone move outwards, in the direction in which it pulled?
--Riding over a dirty road, the wheels of your car acquire a coating of mud, which soon flies off again. How does it fly off?
[Draw schematic on the blackboard].
--What is the acceleration of a stone rotating with speed v around a circle of radius r?
--In the derivation of the formula a = v2/r we neglected a small quantity x. Does that mean that the formula is only approximate, not exact?
--If a stone makes N circuits per second around the center, what is its rotation period, T?
--If a stone makes N circuits per second around a circle of radius R, what is its centripetal acceleration?
Astronauts are subjected to large accelerations during launch and re-entry. The forces associated with such accelerations are often called "g forces" because they are measured in gravities, i.e. the acceleration is measured in units of g, the acceleration due to gravity for which we will use the approximate value 10 m/sec2. In another lesson in "'Stargazers" it was noted that the V2 rocket of World War II started with an acceleration of 1 g and ended at "burn-out", with its mass (mostly fuel) greatly reduced, at about 7 g. The space shuttle (I believe) pulls 3g before burnout, which is quite uncomfortable, even for someone lying flat on the back on a contoured surface. Re-entry has comparable (negative) accelerations. To get astronaut used to taking such forces, they are whirled around during their ground training in a centrifuge, inside a small cabin mounted at the end of a horizontally rotating arm. (Anyone seen such centrifuges on TV?) They are a bit like some amusement park rides, but can create greater stresses, and have TV cameras that monitor the rider.
-- A "human-rated centrifuge" has a radius of 6 meters and creates a 1-g acceleration. How many revolutions per second must it make, and what is its rotation period? Taking g = 10 m/s2,
N2 = 0.04226 N = 0.206 rev/sec (larger than N2, of course, since N<1 !) T = 1/N ~ 5 seconds
--If you double the rotation speed, so that each revolution only takes 2.5 seconds, what will the g-force due to the rotation be?
How is the centripetal force transmitted to the astronaut?
|
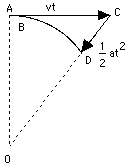 One motion is the continuation of the existing velocity along a straight line (show on the drawing)--the way the weight would move by Newton's first law, if no outside force acted on it.
One motion is the continuation of the existing velocity along a straight line (show on the drawing)--the way the weight would move by Newton's first law, if no outside force acted on it.