|
Triangles come in many shapes. It would be hard to classify triangles of arbitrary shapes, but we note that any triangle ABC can always be divided into two right angled triangles, triangles with one angle equal to 90°. Those are easier to handle. 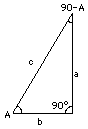
The three angles inside a triangle add up to 180o (we won't prove it here) and therefore, in a right-angled triangle with sharp angles A and B A + B + 90° = 180° Subtracting 90° from both sides A + B = 90° Given the value of just one angle A, the other angle B is completely determined (it equals 90°−A), and so is the shape of the triangle, though not its size. Let the sides of the triangle be named (a,b,c), each matching the name of the angle across from it. The angle A does not determine the length of any side, but it does uniquely fix the ratios between sides. Those ratios have names, and a specific notation exists for writing them: a/c = sin A -- "the sine (or sinus) of A" To tell them apart, just remember: sin A has the side opposite to the angle A on top of its fraction A simple connection exists between the sine and cosine of any angle. For by the theorem of Pythagoras a2 + b2 = c2 Therefore, for any angle A (sin A)2 + (cos A)2 = (a2/c2) + (b2/c2) = (a2 + b2)/c2 = 1 This statement is usually written with the square written sin2A (not sinA2, which might be taken to mean the sine of an angle equal to A2): sin2A + cos2A = 1 Both sinA and cosA must be numbers smaller than 1, for the adjacent and opposite sides of a triangle are always shorter than the side across from the 90° angle (called the hypotenuse, a word dear to the lovers of jokes and puns). As the angle A gets closer and closer to 90° (and B gets smaller and smaller), the triangle becomes increasingly narrow and skinny. The length of side a then approaches that of c, while the length of b becomes very small: therefore as A approaches 90°, sinA approaches 1 and cosA approaches zero. For the derivation of some other values, see the next section. |