A college study unit on motion down an inclined plane, showing that gravity is "diluted" by a factor sinq, where q is the angle of the slope.
An article about the leaning tower of Pisa: Scientific American. . . You can also visit the leaning tower of Pisa and its vicinity--cursor shifts the picture into a 360-degree panorama.
Next Stop: #14 Vectors
############################
Vectors as the Extension of NumbersThe idea of numbers developed very gradually. First came positive integers-- 1,2,3... (not zero, a much more recent addition) to describe countable objects, such as sheep, days, tribe members, etc. The concept of negative numbers might have arisen as an extension of subtraction, or maybe from money--what you owed was negative wealth, red ink in the ledger. Objects which could be divided--for instance, land--brought fractions. Then around 500 BC a student of Pythagoras proved that the number giving the square root of 2 could never be written as a fraction; it did not make sense to them, and therefore we still say these are "irrational" numbers. Between them, integers, fractions and irrationals can describe anything that has a size, a magnitude. But what can describe velocity, which has both a magnitude and a direction? A vector, that's what. Vector additionVelocities can be added. Suppose an airplane flies at 200 mph (or if you wish, kilometers per hour) with a tail wind of 40 mph. How fast does it cover distance on the ground? Easy: for every 200 miles it advances, the wind carries it 40 miles further, so the answer is Graphically, each stretch on the ground or velocity can be represented by an arrow in its direction, its length giving the magnitude--for instance, an arrow AB 200 mm (milimeters) long for the airplane's motion and another one BC 40 mm long, in the same direction, for the wind. To add velocities, put them end to end, as in the top figure here.
and the "arrow addition" (middle figure) confirms it. Next suppose the pilot's course is eastwards, but a 100 mph cross-wind blows towards the north-east: in what direction does the airplane move, and how fast? Intuition does not help, but arrow addition does (bottom figure, not to scale). The general rule is, the combined velocities bring the airplane in an hour to the same spot as when first one motion, then the other, acts alone for an hour. As expected, the direction is somewhere between eastward and northward. All vectors can be added together in this way--like arrows, head to tail. There exists an alternate method, though, often easier to use, and it is described next.
The uses of component vectorsResolving vectors into components can be very useful. Three examples are given below and more follow in section (22a).(a) Adding many vectorsSuppose it is required to add 10 vectors (yes, situations exist...). To perform it the way described earlier, one adds the first two vectors head-to-tail, then adds the third to their sum, then the fourth... tedious business!A faster way is to choose two perpendicular directions, and taking our cue from cartesian coordinates, one will be named here "the x direction" and the other "the y direction". Resolve each vector V into an "x component" Vx along the x direction and a "y component" Vy along the y direction. Now we have not 10 but 20 vectors which need to be added up, but the job is much easier. Of those vectors, 10 are lined up with the x-direction, and vectors in the same direction (like head- and tail-wind velocities in the earlier example of the airplane) add up like ordinary numbers. The same goes for the 10 vectors lined up with the y-direction. The problem is now reduced to two strings of ordinary additionas and subtractions (oppositely directed vectors have minus sign), and only the last step--adding together the grand totals in the x and y directions--requires vector-type addition.
(b) Calculating a vector sumThe head-to-tail addition of vectors allows one to construct their sum graphically. Components allow it to be calculated.Take the earlier example of vector addition--an airplane flying east at 200 mph (its airspeed, its velocity relative to the air), while a 100 mph wind blows towards the north-east. The vector addition triangle of this example is at the bottom of the first figure of this section. Let the x-direction be eastward and the y-direction northward. Then the (x,y) velocity components are, in mph,
This gives the total velocity V. By the theorem of Pythagoras,
giving the magnitude of V as approximately 280 mph, while the sharp angle at point A in the figure (we will name it A, too) satisfies
From which A is about 16.25 degrees. (c) The inclined planeThis goes back to Galileo's experiment. Suppose we have a smooth incline sloping at an angle s (drawing below) and on it a well-greased block, ready to slide down (Galileo used a rolling ball, with which the experiment is easier to perform but harder to calculate, since the kinetic energy is now divided between that of the sliding motion and the one of rotation). If friction is negligible--how fast will the block slide?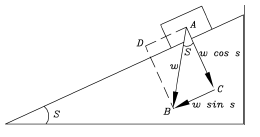
The force of gravity on the block--it has a name, it is called the block's weight W--can be represented by a vertical arrow AB of length W, pointing straight down. That is not the direction in which the block can accelerate. However, the vector AB can also be resolved into two mutually perpendicular forces:
|
Next Stop: #15 Energy
############################
Potential and Kinetic
An interesting thing about the final speed of an object descending (with no friction) from some given height h, along a sloping surface: one can change the slope, one can even change the shape of the surface--yet the final speed v with which it reaches the bottom will always be the same. If it were not for friction, any skier gliding down a snowy hill from the summit to the base should arrive with the same speed, whether the path taken is the easy beginner's slope or the steep experts-only route. Reducing the slope of the surface reduces the acceleration a, but it also lengthens the time of descent, and these two variations cancel, leaving the final speed unchanged. The same speed is also obtained if the object falls vertically from that height h, and in that case it is easily derived, as follows. The duration t of the fall is given by h = g t2/2 Multiply both sides by g: gh = g2t2/2 Then since the final velocity is v = gt one gets gh = v2/2 By the last equation, as the object loses elevation--assuming nothing interferes with its motion--v2 grows, and as noted, this growth does not depend on the path taken. This exchange between h and v2 also works in the opposite direction: an object rolling up an incline loses v2 in direct proportion to the elevation h it gains. A marble rolling down the inside of a smooth bowl gathers speed as it approaches the bottom, then as it shoots up the other side it loses all of it again. If no friction existed, it would rise again to the same height as the one from which it had started. A simple pendulum, or a child on a swing, also trades height for v2 and back again, in the same manner. And bicycle riders are well aware that the speed gained rolling down a hillside can be traded for height when climbing the next slope. It is as if height gave us something with which we could purchase speed, and which later, if the occasion demanded, could be converted back to height. That "something" is called energy. It was already briefly discussed in an earlier section. This back and forth trading suggests that perhaps the sum gh + v2/2 has a constant value: if one part decreases, the other part must get bigger. Is that sum the energy? Not quite. The effort of getting heavy load up a height h is greater than that of lifting a light one. Let us now call the amount of matter in an object its "mass. " It is obviously proportional to the object's weight, but as will later be seen, the concept of mass is more complicated than that. If energy is to measure the effort in lifting a load, it should also be proportional to its mass m. We thus multiply everything by m and write Energy = E = mgh + mv2/2 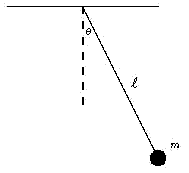
A well-known fact--already hinted at--is that in a system which does not interact with its surroundings, the total energy (denoted here by the letter E) stays the same ("is conserved"). In a pendulum at the extreme point of its swing, v = 0 and therefore the second term above vanishes, while the first term is at its biggest. Then as the mass descends descends, mv2/ 2 increases and mgh drops, until at the bottom of the swing the first term is at its smallest and the second reaches maximum. On the upswing the process reverses, and the sequence is repeated for every swing. Both terms in the equation above have names: mgh is the potential energy, the energy of position, and mv2/2 is the kinetic energy, the energy of motion. The exact number representing E will obviously depend on where h is measured from (the floor? sea level? the center of the Earth? ). Different choices are possible, and each leads to a different value of E: the formula is thus meaningful only if a certain reference height is chosen where h=0. Other kinds of energyTextbooks define energy as "the ability to do work" and they define work as "overcoming resistance over a distance". For instance, if m is the mass of a brick, the force on it is mg and lifting it against gravity to a height h, against the pull of gravity, requires the performance of work W, with W = mgh Dragging that brick a distance x along level ground against the force of friction F similarly requires the performance of work W = Fx For the record, work is measured in joules, after James Prescott Joule (1818-89), a brewer in Manchester, England, whose experiments helped establish the fact that heat was a form of energy (see further below) and not some mysterious fluid permeating matter. Since any such work can be performed by a machine, one can also loosely define energy as anything that can cause a machine to turn. |
| Devices or processes that convert energy from one form (column) to another (row) | ||||||
|---|---|---|---|---|---|---|
| - | Kinetic | Potential | Heat | Light | Chemical | Electric |
| Kinetic | ***** | Pendulum | Rocket Nozzle | Solar sail | Muscles | Electric motor |
| Potential | Pendulum | ***** | Steam boiler | x | x | Elevator winch |
| Heat | Friction | x | ***** | Solar heater | Fire | Electric stove |
| Light | x | x | Lightbulb, Sun | ***** | Firefly light | Light emitting diode |
| Chemical | x | x | Quicklime kiln | Green plants | ***** | Car battery |
| Electric | Windmill power | Hydroelectric power | Thermocouple | Solar Cell | Flashlight battery | ***** |
|
Energy is also measured in joules. In many ways it resembles money: it is a currency in which all processes in nature must be paid for. Just as money can come in dollars, pesos, yen, rubles or liras, so energy can come in many forms--electricity, heat, light, sound, chemical, nuclear. The expression for the total energy of a system of objects can be written E = (potential) + (kinetic) + (electric) + (heat) + . . . where "kinetic" for instance stands for the sum of mv2/2 for all the component parts. And it is still true that if the system does not interact with the outside, the total value of E is conserved. It is also true that in most cases, with proper tools, one form of energy can be converted into another: light shining on solar cells generates electricity, which can turn the motor of a fan, providing the kinetic energy of rotating blades, or run a radio, producing sound. UnitsLike currencies, different kinds of energy have a certain exchange rate: in the exchange between kinetic or potential energy and heat, for instance, one calorie equals about 4.18 joules. The chemical energy of food is also measured in calories, though one should note these are "big" calories or kilocalories, each equal to 1000 of the small kind. The rate at which energy is supplied or used is called power and is measured in watts, after the inventor of the modern steam engine, the Scotsman James Watt (1736-1818): an energy supply providing one joule per second gives one watt of power. Thus a 60-watt bulb provides 60 joules each second--about as much as a biker pedaling up a hill. Bills for electric energy, sent out by power companies, are usually calculated at so many dollars, pesos, yen etc. per kilowatt-hour (kwh)--the energy of one kilowatt or 1000 watt, supplied for one hour. Since the hour has 3600 seconds, it follows that one kwh equals 3 600 000 joules. HeatWhen a bank changes money from one currency to another, it usually charges some percentage as the cost of the transaction. The same happens in the exchange of energy from one form to another: you always get less than what you put in. The marble sliding down the side of the bowl, for instance, always rises on the other side to a lower elevation than the one it started from. The missing energy is not lost, however, but ends up as heat. Heat is the "soft currency" of the energy universe: it is possible to convert heat to other forms of energy (in a steam engine, for instance), but one can never get the full value. That, essentially, is the "second law of thermodynamics," a fundamental law related to the nature of heat. The missing amount not only remains as heat, but becomes heat at a lower temperature, from which only an even smaller fraction can be converted into other forms. It would solve all of mankind's energy problems if, for instance, one could extract the heat energy of the oceans, leaving them slightly cooler and converting the extracted heat to electricity; but the second law tells that it cannot be done. |
| . | Bar | 100 gr. |
| Energy Kj | 885 | 2300 |
| ..........Kcal | 210 | 550 |
| Protein | 2.7 gr | 7.1 |
| Carbohyd. | 20.8 | 53.9 |
| Fat | 13.2 | 34.2 |
Next Stop: #16 Newton and his Laws
############################
Isaac Newton was born in 1642, the year Galileo died. Almost all his creative years were spent at the University of Cambridge, England, first as a student, later as a greatly honored professor. He never married, and his personality continues to intrigue scholars to this day: secretive, at times cryptic, embroiled in personal quarrels with some scholars yet generous to others, bestowing his attention not just on physics and mathematics, but also on religion and alchemy. The one thing about which everyone agrees is his brilliant talent. Three problems intrigued scientists in Newton's time: the laws of motion, the laws of planetary orbits, and the mathematics of continuously varying quantities--a field nowadays known as [differential and integral] calculus. It may be fairly stated that Newton was the first to solve all three. No wonder that the poet Alexander Pope, who lived in Newton's time, wrote:
|
This section discusses two concepts on which they are based: |
|
|
However... "to own a concept," you need to go beyond formal definitions and get an intuitive idea of what it means. Science often develops like this, too. You start with an improvised "working definition," then when you understand it better, you replace it with a more precise meaning. That approach is used here. Explanations may be longer--but reading is easier on the student than the frustration of not being able to understand.
As a working definition, let us call "force" that which causes or changes motion.
One force everyone is familiar with is the weight of objects, the force which tries to make them move downwards, to fall towards the center of the Earth. We may thus measure force (at least now, temporarily) in kilograms of weight, and view as force anything that can be matched by weight. For instance, a spiral spring can be compressed or stretched by weight, so it is fair to say that it, too, exerts a force when compressed or stretched.
Based on hindsight--on experience with forces noted by many people, including Newton--we may distinguish two basic situations in which force creates motion:
It was Newton's insight that in the absence of external resistance, motions in a straight line and at constant speed would continue indefinitely. No force is necessary. That is Newton's first law of motion:
A hockey puck sliding on a sheet of ice can travel great distances, and the smoother the ice, the further it goes. Newton realized that what ultimately stopped such motions was the friction of the surface. If an ideally smooth ice could be produced, with no friction at all and extending to unlimited distances, the puck would continue indefinitely, never stopping, in the same direction and with the same velocity as the ones with which it had started.
What a force can do in the absence of resistance is increase the velocity of an object -- accelerate it.
However... even without external resistance, there remains an internal resistance, by the object itself. An astronaut pushing a one-ton satellite out of the cargo bay of the space shuttle quickly finds that even though the satellite seems "weightless," it is not easily moved. Given a push by the astronaut, it will indeed start to move, but v-e-r-y v-e-r-y s-l o-w-l-y . It resists being put in motion, and once moving, it resists just as much being slowed down or stopped.
Newton named that internal resistance inertia.
Obviously, inertia increases with the amount of matter. A bowling ball is harder to get moving and harder to stop than a hollow rubber ball of the same size.
The bowling ball is also heavier, that is, it is pulled downward with greater force: but weight is an effect of gravity, while inertia is not. The two seem to go together in some way, and the next section examines this further.
Tidbit:
Supertankers (" Large Crude Carriers") are large ships which can carry 150-300,000 tons of crude oil, at about 18 mph (nearly 30 km/h). Such a heavy load carries an enormous inertia. Even with the engine thrown into reverse, supertankers take a mile or more to come to a stop, and are equally hard to turn around. Yet a wreck must be avoided at all costs, because oil spills cause enormous ecological damage.
Supertanker officers are therefore trained in a facility in the Netherlands (Holland), piloting a small replica of a supertanker around a lake. The replica is about 25 feet long, and the officer sits in it with just the head showing. Although small, the boat is heavy and underpowered. It only has a small engine, the size of an outboard engine used by small boats, and its rudder is also to scale, small. Therefore, even though the boat has far less speed than a supertanker, it is also hard to stop and control (in the limited space of the lake), and can therefore train officers in the handling of heavily loaded ships.
The portrait of Newton at the start of this section, perhaps his best likeness, was painted in 1689 by Godfrey Kneller, and for 150 years its existence was known only to a few. For its story and for some other paintings of the man, see " Images of Newton, " Endeavour, 24 p. 51-52, No. 2, 2000.
|
Next Stop: #17 Mass
############################

Galileo noted that light and heavy objects fell at the same rate. Why? An iron cannonball and a wooden ball of the same size, when dropped from the leaning tower of Pisa, hit the ground together. But the force on the cannonball--its weight--is larger. Why doesn't it fall any faster? |
| Newton gave the correct answer: heavier objects also have greater inertia. Not only is the cannonball pulled down with a force that is (say) 10 times larger, it also resists acceleration 10 times more strongly. Newton expressed it in a mathematical formula--"Newton's second law of motion," described in a later section. But simply stated, the result is that both objects fall at the same rate (ignoring air resistance). |
|
This introduces yet another concept, that of the mass of an object--loosely defined as the amount of matter it contains. Inertia is proportional to mass, weight is also proportional to mass, too, so both go together. The difference is that inertia is an inherent property of matter, while weight also depends on gravity. A person weighing on Earth 120 pounds (or 120 kilograms, if you wish) weighs only 40 on Mars and 20 on the Moon.
Still, the easiest and most common way of measuring mass is by weighing, which uses gravity. In a two-pan balance, we compare the weight of an unknown object to that of a set of known weights: Because of this, mass is usually measured in kilograms, even though these are also units of weight. In a one-pan balance, like the one pictured here, the comparison weights are fixed, but by sliding them to different distances from the pivot, the same result is achieved.
Measuring Mass on a Space StationIn 1973 NASA put in orbit the space station Skylab, and its experiments included a careful monitoring of the health of the crew. One important quantity was the body mass of the astronauts. Here on Earth it would be called "body weight" and would be measured by weighing a person on scales. However, scales would not work on a space station. They use gravity, balancing its force on the astronaut's body against a calibrated spring or against the force of gravity on some calibrated weights. It is not correct to say that gravity does not exist on an orbiting spacecraft (if it did, the spacecraft would fly away, never to return). Rather, in the "zero g" environment of the space station, gravity is already doing all it can in moving the station in its orbit, and none of it is evident inside the station. Since the orbit is curved, the first law is not violated by requiring a force to maintain it. How can mass be measured there? One gets a clue from clocks, all of which need some sort of device that gauges the passage of time. Pendulum clocks--always kept upright--use gravity, but mechanical wristwatches depend on a balance wheel, turning periodically back and forth--clockwise, then counter-clockwise, then clockwise again--against a spiral spring. Gravity is not involved. Modern electronic wristwatches replace the wheel with a vibrating quartz crystal, acting somewhat like a tuning fork: the motion is much faster, but transistor circuits can easily count the vibrations, which are very stable. |
 |
|
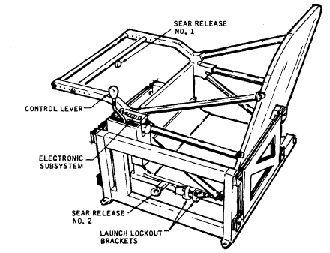
The frequency of the balance wheel--its number of back-and-forth oscillations--depends on its rotational inertia. Astronauts aboard "Skylab" used something similar--but with a simpler back-and-forth motion, rather than a rotation. It resembled a porch glider, a seat which could glide forward and back against springs (see drawing above). Since the oscillation is opposed by inertia, the greater the mass, the slower is the process, and by measuring the frequency of oscillation, a fair idea of body mass could be obtained. For further details on mass measurements aboard "Skylab," see the next section.
Optional: Gravitational Mass and Inertial MassYou will notice that the mass of an object can be measured (that is, compared to the mass of one liter of water) in two different ways. Some physicists accordingly distinguish gravitational mass mg from inertial mass mi. Using scales and the local force of gravity, one can determine gravitational mass; or else, one might dispense with gravity, like the astronauts aboard Skylab, sand measure the "inertial mass," and in principle they may differ. One could imagine a universe where the two are not proportional (whenever they are proportional, a choice of units can make them equal). In that universe a chunk of lead may have (as in our own universe) about 4 times the weight of a chunk of aluminum of the same size and shape, but only twice the inertia. Two-pan scales will give the chunks weights with a ratio 4:1, but devices like the ones of the sections that follow will only give a mass ratio 2:1. As it happens, our own universe is not like this, but the two masses are always the same. Around 1900 the Hungarian physicist Roland Eötvös (Lorand in Hungary; see picture) compared the two, using extremely sensitive instruments. He concluded that they were the same to an accuracy of many decimals, and that equality became one of the foundations of physics, especially of the general theory of relativity. Some years ago it was suggested that a small difference existed, hinted by small differences in results by Eötvös for different substances (even though the variation he found was within error bounds). This lead to a search for a "5th force" modifying gravity, but careful measurements disproved the existence of such a force. |
What if you could lose weight without losing mass? A century ago H.G. Wells wrote a humorous and delightful fantasy story around this possibility, The Truth about Pyecraft.. Look it up!
Additional details: #17a Mass Measurements aboard Space Station Skylab
Next Regular Stop: #18 Newton's Second Law
############################
NASA's biggest rocket was the giant Saturn V, developed by NASA for the lunar missions of project Apollo. Following several successful moon landings,NASA decided to use its last Saturn V not to fly to the moon but to place in low Earth orbit a large space station, named Skylab. (For a picture and some related links, click here or here) The station weighed close to 100 tons and was sent into orbit on May 14, 1973. It was followed that year by three manned flights using the smaller Saturn IB, each carrying 3 astronauts for a prolonged stay aboard Skylab. Those missions, designated Skylab missions 2, 3 and 4, lasted 28, 59 and 84 days, respectively. Today a back-up Skylab module is open to visitors in the National Air and Space Museum of the Smithsonian Institution in Washington(picture on the left). The orbit of Skylab was not high enough to avoid atmospheric friction, and over the years the station gradually lost altitude. A plan was made to to push it to a higher orbit with the space shuttle, but the first shuttle was not ready on time. Meanwhile the 11-year sunspot cycle advanced towards its peak, bringing a significant growth in the the soft X-rays and extreme ultraviolet (EUV) emitted by the Sun. Such radiations are quickly absorbed in the high layers of the atmosphere, which are markedly heated by the process. That heating makes the upper atmosphere expand upwards, increasing air resistance to low-orbit spacecraft, and as a result Skylab re-entered the atmosphere on July 11th, 1980. Most of it was burned up by atmospheric friction, but some pieces were recovered from the Australian desert. 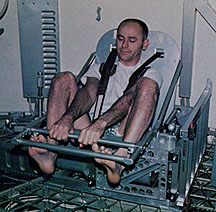
Mass measurements aboard Skylab were part of the medical experiments conducted there. Prior to the Skylab mission it was observed that both US and Russian astronauts returning from space had lost weight, and NASA worried whether this implied some physical deterioration which could grow worse on longer flights. Several reasons were suggested for this loss. Because of gravity, blood pressure is higher in the legs (just as water pressure is higher at the foot of a watertower than it is halfway up), causing a counterpressure to be exerted by blood vessels there. Some believed that in a zero-gravity environment, the extra load opposed by this counterpressure did not exist, causing more blood to be pushed into the upper body, and the body, sensing the extra blood, eliminated it, causing a loss of fluids. Others blamed unnatural meal arrangements and loss of appetite due to nausea (which some astronauts developed, but others did not). Still others felt that work in space tended to be unusually stressful. To better observe the process, Skylab carried three mass-measuring devices--two small ones (experiment M074) for measuring the intake and outgo of each astronaut, and a large one (experiment M172) with an oscillating chair, designed for daily monitoring of the weight of the astronauts. The motion of the oscillating mass was tracked electronically, typically over three back-and-forth oscillations, and from this the instrument derived the oscillation period T. Theory predicted that T would be proportional to the square root of the oscillating mass; this was confirmed by calibrations in space, using previously weighed objects, and those calibrations suggested that when carefully performed, such mass measurements were accurate within 0.1%. Measuring body mass in the M172 chair (see illustration) was not a simple matter. The human body is not rigid, and any internal motion--even breathing--could affect the oscillation of the chair. After emptying their pockets, astronauts would climb into the chair, always wearing a suit which had been weighed before the flight. They would then be strapped in rigidly, brace their feet against a bar at the front of the chair, grab hold of another such bar with their hands, hold their breath and then release the seat by pushing a trigger on the hand bar. Astronauts of Skylab-2 lost 3-6 pounds during their one-month stay, and measurements of intake suggested they were not eating enough. On Skylab-3 food rations were therefore increased, and additional excercises were also ordered, to make sure that "body muscle was not exchanged for fat." Weight loss was comparable, even though the stay in space was twice as long, and it was noted that most of the loss occured in the first five days. The Skylab-4 crew was given still more food and more excercises. All three astronauts of that group lost mass during the first 10 days, but for the remaining 74 days they held their own or even gained mass back. As for the reasons suggested for the mass loss, apparently all three of them contributed. (Credit: Most of this material is based on the transcript of a talk "Physiological Mass Measurement in Skylab," presented by astronaut-scientist William E. Thornton, MD, and by Colonel J. Ord, USAF, at the Skylab Life Sciences Symposium, Johnson Space Center, August 27-9, 1974. I thank Joan Ferry of the Johnson Space Center History Archive for making this and other documents available. ) |
On the effects of weightlessness in a space station: " Weightlessness and the Human Body" by Ronald J. White, Scientific American, September 1998, p. 58.
" Skylab, Our First Space Station" edited by Leland F. Belew, NASA special publication SP-400, 1977. The above illustration of the M172 mass-measuring chair appears on page 116.
" Skylab, Outpost on the Frontier of Space" by Thomas Y. Canby, National Geographic, October 1974. The "chair" shown above also appears there, at the top of the general view of Skylab on page 466.
Classroom experiment: #17b Comparing Masses without the Use of Gravity
Next Regular Stop: #18 Newton's Second Law
############################
|
With only the simplest equipment, you too can perform mass measurements similar to the ones aboard Skylab.
|
You will need:
|
Instructions
|
|
The theory predicts that the oscillation period should be proportional to the square root of the oscillating mass, including the mass of the clip. Note that gravity plays no part here: the oscillation period would be the same on the Moon or in zero-g. Denoting square root by SQRT, we have
|
|
(T2/T1) = SQRT(m2+m0)/SQRT(m1+m0) = SQRT[(m2+m0)/(m1+m0)].
|
|
("The ratio of square roots is the square root of the ratio"). Muliplying each side by itself: (T2/T1)2 = (m2+m0)/(m1+m0). If we were in space, measured T1 and T2, and knew the masses m1 and m0, then we could calculate an unknown mass m2.
|
|
Weights: m1 = 50 gr, m2 = 120 gr, m0 = 10 gr. The number of oscillations counted in a 10-second period was: with m1, 20 oscillations, with m2, 13.5 oscillations. Then
|
|
T1 = 10 sec/20 = 0.5 sec T2 = 10 sec/13.5 = 0.74074 sec. so that
(T2/T1)2 = 2.195 should equal (m2+m0)/(m1+m0) = 130/60 = 2.167 |
|
This agreement is probably better than such a crude experiment deserves, considering that the mass of the sawblade itself was ignored.
|
Next Stop: #18 Newton's Second Law
############################

For more money bills with famous physicists, click here |
Summary--up to here:
|
The MKS System and the "newton"Consider free fall due to gravity. The force of gravity is proportional to mass m, so we can write
where g is the acceleration of gravity, directed downwards. Yes, proportionality allows one to add on the right some constant multiplier, but we won't, because now we want to define some units of F. All quantitative formulas and units in physics depend on the units in which three basic quantities are measured--distance, mass. and time. Let us therefore choose from now on to measure distance in meters, mass in kilograms and time in seconds. That convention is known as the MKS system: as long as one's formulas contain only quantities derived by that system, they will be consistent and correct. But watch out... if by mistake you mix MKS units with grams or centimeters (or pounds and inches), and you may end up with some mighty strange results! In the MKS system g varies from 9.78 m/s2 on the equator to 9.83 m/s2 at the poles. Equation (1) not only shows that weight is proportional to mass, but--assuming it is measured in kilograms--it introduces a unit of F, named (no surprise!) the "newton." By that equation, a force of one newton acting on one kilogram of mass accelerates it by 1 m/sec2, so the force of gravity on one kilogram of mass is about 9.8 newtons. Earlier this was called "a force of one kilogram of weight, " a convenient unit for rough applications, but not for accurate ones, because of the variation of g around the globe.
Newton's Second LawWe are at the point where the dependence of acceleration on force and mass can be expressed in numbers. Lord Kelvin, leading British scientist in Queen Victoria's era, was quoted as once saying
By Newton's second law, the acceleration a of an object is proportional to the force F acting on it and inversely proportional to its mass m. This may be written
The acceleration a of an object is proportional to the force F acting on it and inversely proportional to its mass m. Actually, two things should be noted. First, "proportional" means that until we decide what units to use in measuring a, F and m, we should allow some constant number k multiplying F, so it would be more accurate to write a=kF/m. Second, both a and F have not only magnitudes but also directions--they both are vector quantities. Denoting vectors (in this section) by bold face lettering, Newton's second law should properly read
This expresses the earlier statement "accelerates in the direction of the force." Now suppose a is in m/s2, m in kilograms (kg) and F in newtons. and suppose the equation derives the acceleration of a falling object of mass m. Then by (1) F=mg, giving
However, we already know the acceleration of a freely falling object: it is just g, not any less or more: so in these units, k=1, and since multiplication by 1 changes nothing, we can drop k and simply write
but equation (4) is the form in which it is usually used--F and m are the inputs, a is the result. The example below should make it clear.
Example: the V-2 RocketThe V-2 military rocket, used by Germany in 1945, weighed about 12 tons (12,000 kg) loaded with fuel and 3 toms (3,000 kg) empty. Its rocket engine created a thrust of 240,000 N (newtons). Approximating g as 10m/s2, what was the acceleration of the V-2 (1) at launch (2) at burn-out, just before it ran out of fuel?Solution Let the upwards direction be positive, the downwards direction negative: using this convention, we can work with numbers rather than vectors. At launch, two forces act on the rocket: a thrust of +240,000 N, and the weight of the loaded rocket, mg = -120,000 N (if the thrust were less than 120,000 N, the rocket would never lift off!). The total upwards force is therefore
and the initial acceleration, by Newton's 2nd law, is
The rocket thus starts rising with the same acceleration as a stone starts falling. As the fuel is used up, the mass m decreases but the force does not, so we expect a to grow larger. At burn-out, mg = - 30,000 N and we have
giving The fact that acceleration increases as fuel is burned up is particularly important in manned spaceflight, when the "payload" includes living astronauts. The body of an astronaut given an acceleration of 7 g will experience a force 7 times its weight, creating excesive stress (3-4 g is probably the limit without special suits). It is hard to control the thrust of a rocket, but a rocket with several stages can drop the first stage before a gets too big, and continue with a smaller engine. Or else, as with the space shuttle and the Atlas rocket, some rocket engines are dropped while others continue operating. |
Next Stop: (18a) Newton's 3rd Law
############################
Newton's 3rd law may be formally stated:
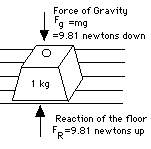
"Forces always occur in pairs. If object A exerts a force F on object B, then object B exerts an equal and opposite force -F on object A" or in slogan style: Note the important provision: two objects must be involved! There exists a whole set of situations where two equal and opposite forces act on the same object, canceling each other so that no acceleration (or even no motion) occurs. This is not an example of the third law, but of equilibrium between forces. Some examples: |
In contrast, Newton's 3rd law always involves more than one object.
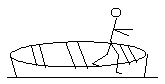
Those familiar with small boats know that before jumping from a boat to the dock, it is wise to tie the boat to the dock first, and to grab a handhold on the dock before jumping. Otherwise, even as you jump, the boat "magically" moves away from the dock, possibly making you miss your leap or pushing the boat out of reach. It is all in Newton's third law: as your legs propel your body towards the dock, they also apply to the boat an equal force in the opposite direction, which pushes it away from the dock. The Bicycle A more subtle example is afforded by the bicycle. It is well known that balancing a bicycle standing still is almost impossible, while on a rolling bike it is quite easy. Why?
A more subtle example is afforded by the bicycle. It is well known that balancing a bicycle standing still is almost impossible, while on a rolling bike it is quite easy. Why?Different principles are at work in each case. Suppose you sit on a bike that stands still, and find it is leaning to the left. What do you do? The natural tendency is to lean to the right, to counterbalance the lean with your weight. But in moving the top of your body to the right, by Newton's 3rd law you are actually pushing the bike to lean more to the left. Maybe you should lean to the left and push the bike back? It might work for a fraction of a second, but now you are really out of balance. No way! On a rolling bike, balance is kept by a completely different mechanism. By slightly turning the handlebars right or left, you impart some of the rotation of the front wheel ("angular momentum") to rotate the bike around its long axis, the direction in which it rolls. That way the rider can counteract any tendency of the bike to topple to one side or the other, without getting into the vicious circle of action and reaction. To discourage thieves, some bikes contain a lock which clamps the handlebars in a fixed position. When such a bike is locked in the forward-facing direction, it can be rolled by a walking person, but it cannot be ridden because it cannot be balanced.
(Optional Addition)
Newton's laws were introduced here in the traditional way--through the concepts of mass and force (Newton actually formulated the second law in terms of momentum, not acceleration). Ernst Mach, who lived in Germany two centuries after Newton, tried to avoid new concept and formulate physics only in terms of what can be observed and measured. He argued that Newton's laws boil down to one law:
Read it again, if you will: no mention of force or mass, only of acceleration, which can be measured. When a gun acts on a bullet, a rocket on its exhaust jet, the Sun on Earth (and on the scale of the distance separating the two, Sun and Earth can be viewed as compact objects), the accelerations are always oppositely directed. Mass and force are now readily derived. If one of the objects is a liter of water, its mass is defined as one kilogram. If it then acts on another object (perhaps with the water frozen into ice, for the purpose of the experiment), then the ratio of its acceleration aw to the acceleration a of the other object gives the object's mass m. And a force of 1 newton is defined as the one that causes 1 kg an acceleration of 1 m/sec. |
Next Stop: #18b Momentum
############################
A cannon weighing 1 ton (metric ton, 1000 kilograms) fires a 10 kg shell at 1000 meters/second. With what velocity does the cannon recoil?
RecoilAt first sight something is missing here. How can Newton's laws be applied to a problem where neither force nor acceleration are given? But hold on!Let us start the solution process by collecting all the given information. Denoting with subscript 1 quantities related to the shell and with subscript 2 those related to the cannon, we have
Shell: m1 = 10 kg
v1 = 1000 m/s
When a problem involves unspecified quantities, the best strategy usually is to give each of them a name and hope for the best: either their actual values can be found, or they will "drop out," showing they are not essential to the solution. Such "miracles" may happen if all the information needed for the answer is already given. You will need some experience, though, to judge whether or not all vital pieces of information are already on hand. What missing quantities are needed by the equations? For starters, the forces (F1, F2) on the shell and cannon, the magnitudes of their accelerations (a1, a2) which we assume to be constant (we know they are in directions opposite to each other), and the length of time t during which they act. We now collect equations: From the second law
F2 = m2a2
which removes forces from the picture. Also:
Divide left by left and right by right in the last equation, to get
which removes the time t. Going back to equation (1), divide both sides by a1m2. Then
Substitute from (2) to (3), or vice versa, and suddenly the accelerations, too, are gone. All that is left is
where everything is known except for the recoil velocity v2. Its value is isolated by multiplying both sides by v1
Our final equation (4) becomes more symmetric if all fractions are eliminated. Multiplying both sides by the product (m2v1) of the denominators gives
The quantity "mass times velocity" (or "the product of mass and velocity") is called momentum (plural: momenta) and is often denoted by the letter P. One way of interpreting the last equation (5) is to state that the momentum given to the cannon equals the momentum given to the shell.
Conservation of MomentumActually, the momentum P, like the velocity v, is a vector quantity. Suppose we regard velocities in one direction as positive and in the opposite direction as negative. Then
|
|
v1= 1000 m/s
P1 = m1v1 = 10 kg x 1000 m/s = 10,000 kg-m/s v2= - 10 m/s P2 = m2v2 = 1000 kg x (- 10 m/s) = -10,000 kg |
|
Before the gun was fired, neither mass had any velocity and therefore the total momentum P = P1 + P2 was zero. Afterwards, evidently, the total momentum remained zero. This is a general property (and yet another formulation of Newton's laws) and can be stated as In a system of objects subject to no forces from the outside, the vector sum of all momenta stays the same ("is conserved"). This also works when three or more objects are involved and each moves along a completely different direction. For instance, "the shells bursting in the air" of the US anthem had the same momentum as the collection of fragments and gases produced imediately after they burst, before air resistance had its say. This is also the principle by which a rocket operates--as it throws mass backwards in a fast jet of gas, it receives an amount of forward momentum equal to the backward momentum given to the jet.
EnergyWhen the cannon recoils, it receives as much momentum as the shell. How is the energy E shared? Since
and for the cannon
Very unequal sharing! The cannon, 100 times massive, receives 100 times less energy. Is that the rule?
Dividing
Substitute equation (1) in the numerator, then cancel (m2v2) above and below to get
By (4), inverted
hence
The lighter mass always receives the lion's share of the energy! |
Next Stop: #18c Work
############################
|
The concept of Work is closely related to that of energy. In fact, the formal definition of energy is "the capacity to perform work." Let us see what this means.
Work is associated with forces that overcome resistance. The work W performed while overcoming a resisting force Fover a distance xis defined as Ftimes x
Things to note: Fmust oppose the motion. If the direction of the vector F differs from the direction of x,then Fmust be resolved into components parallel and perpendicular to x (in the manner discussed in section 14) and only the parallel component directly opposing the motion is used in the formula for W.
Suppose we lift a weight Aof mass m a distance h(for height) from the floor to the table (Figure 1). The force we must overcome is
That, however, is just the potential energy added to the weight! We could tie the weight by a string to a similar weight on the floor--denoted B--and pass the string over a pulley. Then--with an ideal pulley having no friction, and an ideal string having no weight--if the mass on the table is pushed over the edge, the slightest downward push will make it descend all the way to the floor, while B is raised to the level of the table. Work W was performed in raising mass B, while mass A has given up its potential energy. That shows energy is indeed "ability to perform work": potential energy was given up, and in return work was performed. The work performed in raising B was again invested in potential energy. With ideal pulleys, strings etc., that energy again equals W, illustrating the conservation of energy. In an ideal set-up with no losses, this energy could be used to raise A to its previous height. Note that our working definition "energy is anything that can turn a machine" also holds, since a dropping weight could indeed turn a machine. Energy is always preserved but--as seen in an earlier section--not always in a usable form. Suppose the weight A is tied, not to an equal weight on the floor, but to a block of concrete on a table (Figure 2). If the force of sliding friction of the block on the tabletop is exactly equal to mg, then dropping A allows the block to slide a distance h and overcome F along it. But now the potential energy mgh has been converted to heat, generated by friction. This is energy too--but energy dispersed on the molecular level, hard to convert back to work. And as noted in section 15 on energy, even with ideal devices and substances, physics can at most promise the recovery of a certain fraction of that energy, never all of it. |
|
Tidbit: The two weights A and B in the first drawing illustrate the principle of the funicular railways, short railways with a straight track leading steeply up a hill or mountain. Funicular railways always have two short trains (sometimes, of a single carriage each), connected by a steel cable. The cable goes from one train to the mountain top, where it wraps a few times around a drum turned by a motor, and then it continues down again, to the other train. Because the trains are linked, when one goes up, the other descends, and by giving up its potential energy, it helps pull the other one upwards. Any in-between stations must always be coordinated, so that when the ascending train stops at station X, the descending train stops at station Y (and later, with the ascending train at Y, the descending one is at X). When one train is reaches the bottom station, the other reaches the top station. One would think that two tracks are needed, one for each train. Actually, one track is enough, if halfway up where the trains meet, a short double section is inserted, with switches that automatically route the trains to a separate tracks, allowing them to pass safely. Gondolas suspended from cables and taking tourists to the tops of scenic mountains may also be connected in pairs like this, but they always hang from separate cables. |
Optional Section: #18d: Work Against an Electric Force: The Van de Graaff Generator
Next Regular Stop: #19 Motion in a Circle
############################
|
Many textbook examples on work are based on overcoming gravity--as for instance in preceding section #18. If you lift a brick from the ground to the table, you perform (or "invest") work and gain potential gravitational energy, and this energy can be converted back, to the work of raising a different brick. But nature also has other forces, such as the electric force.
The Electric ForceOrdinary matter consists of negative electrons and positive atomic nuclei, and their electric charges attract each other. That is what holds atoms together! Usual matter has equal amount of positive and negative electric charge.However, by rubbing (say) glass with a dry wool cloth, electrons can be removed, leaving it positive, while the same electrons are picked up by the cloth which therefore gets a negative electric charge. Other materials (like amber) attract electrons from the cloth and get negative when rubbed. Objects with positive charge attract those with negative charge, but two positively charged objects, or two negative ones, repel each other. There exist other ways of detaching electrons from matter, but the process is self-limiting. Suppose you deposit extra electrons on an object: it the becomes negatively charged, strongly repelling any additional electrons and by this not allowing any addition to its charge. Mathematically this can be expressed by a negative "electric pressure" (also known as negative "voltage", since it is measured in units called volts) which pushes back any other negative charges. If that voltage gets too high, electrons may be pushed off as a spark, and a symmetric effect exists with positive charge, which can forcibly pull electrons from surrounding material. That is what happens in lightning, when processes in a thundercloud (see below) separate electric charges and create high voltages. In general, sharp points create sparks even at low voltages, while large smooth spheres resist sparking. The interesting thing to note is that the repelling (or attracting) force only exists outside the sphere: inside a hollow enclosure no electric force or voltage can be observed. You may be pleased to know that if you sit inside a closed aluminum airplane cabin when it is struck by lightning, the metal enclosure protects you from any electric effects.
Van de Graaff's inventionIn 1929 Robert Van de Graaff in Princeton found a new way of charging a hollow sphere to high voltages. He mounted it on top of a high insulating column, inside which a rubber belt ran around two pulleys--one inside the sphere, the other (turned by a motor) in the base. Also in the base was a source of negative voltage, attached to a series of sharp points, which sprayed negative electric charge onto the belt. Positive electric charge can also be sprayed--but here it is convenient to talk about electrons. The other side of the voltage source was connected to the ground, so that as electrons were sprayed off, others came up and replaced them, leaving behind no excess positive charge.Since rubber does not conduct electricity (that is, does not allow electric charges to move from one point to another, as a metal would), the belt carried its charges into the sphere, inside which another series of sharp points, placed close to the belt, skimmed them off. Wires connected the points to the sphere, so the charge distributed itself all over it. Gradually, the sphere became more and more negative. That did not prevent the unloading of electrons inside the hollow interior, but the voltage outside, however, could rise to a few million volts. When that voltage became high enough, a lightning-like spark usually leaped to the ground or to some convenient metal target. The Boston Museum of Science has such machines, and uses them to provide visitors with impressive demonstrations.
Energy and Work DoneAs the spheres charge up, they accumulate electric energy. Where does that energy come from? Simple. We said that even when the sphere is charged up to a million volts, inside it electric forces are absent, posing no obstacle to skimming charge off the belt. But outside it, such forces do exist! As the belt carries negative electric charge towards the sphere, it must overcome the repelling force F of the negative charge already on it ... and perform work! The motor must overcome that repulsion, and is therefore the energy source. A student turning the lower pulley by a crank could also provide energy, but should watch out for those sparks!
|
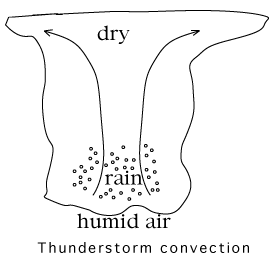
Lightning(I am grateful to Prof. Martin Uman of the U. of Florida in Gainesville for correcting the initial version of this section).Could a similar process be responsible for the high voltages that cause lightning in thunderstorms? A thunderstorm cloud is essentially a violent upward flow of humid air. Rising air expands and cools, but the surrounding air at higher levels is cooler, too: what determines whether a flow continues to rise or not is whether it is warmer or cooler than the air around it. The rising flow in a thunderstorm gives up humidity in the form of rain (cooler air cannot hold as much water) and that process, it may be shown, provides extra heat. The water therefore keeps the air warmer than its surroundings, and it keeps rising. The result is motion in two directions: a wind blows upwards, and meanwhile raindrops fall through it towards the ground. Some raindrops are blown upwards by the wind, to higher levels where they freeze, and this too helps keep the air warmer. (Orange growers in Florida spray water when temperatures drop below freezing: the water freezes and falls to the ground, while orange trees are kept warmer.) Ultimately they may come down again as hail, commonly associated with thunderstorms. Big hailstones apparently start as regular hail, collect more water as they fall, then are blown upwards again. Freezing is important, because observations suggest that thunderstorm electricity is created not by liquid water, but by ice. The ice fragments created in the cloud come in various sizes: while large ones tend to fall down, small slivers are generally blown upwards, and the two kinds collide. The collisions may separate charge (a bit like frictional electricity): the little slivers tend to lose electrons and become positive, and because the total electric charge is zero, those lost electrons give a negative charge to the larger ice particles. The magnitude of the effect depends strongly on temperature--even the sign of the transferred charge reverses for some temperatures--and this leads to additional features of lightning generation. Because the two types of ice fragments have opposite charges, they attract each other: but gravity pulls the bigger ones down, while the wind blows smaller slivers even higher, and in separating the two types, these two forces perform work against the electric attraction. The situation is therefore somewhat similar to Robert Van de Graaff's machine, except that there the rubber band overcomes electric repulsion, while here, the forces of the wind and of gravity overcome an attraction. Still, work is work, and by performing it the process increases the energy stored in the system. The top of the cloud, where the little slivers end up, becomes charged to a high positive voltage, until the air cannot contain the growing electric charge any more, and... FLASH! BOOOOM!
Exploring FurtherA site picturing the Van de Graaff Generators of the Boston Museum of Science. Built by Robert Van de Graaff after he became a professor at MIT, they were later given to the museum. Their story, illustrated by unique photographs, is found here, while the life of Prof. Van de Graaff is described here.A site concerning lighning electrification. |
Next Stop: #19 Motion in a Circle
Author and curator: David P. Stern, u5dps@lepvax.gsfc.nasa.gov
This joined version created 8 June 2001