|
Pythagoras of Samos was a Greek philosopher who lived around 530 BC, mostly in the Greek colony of Crotona in southern Italy. According to tradition he was the first to prove the assertion (theorem) which today bears his name:
A right angle can be defined here as the angle formed when two straight lines cross each other in such a way that all 4 angles produced are equal. The theorem also works the other way around: if the lengths of the three sides (a,b,c) of a triangle satisfy the above relation, then the angle between sides a and b must be of 90 degrees. For instance, a triangle with sides a = 3, b = 4, c = 5 (inches, feet, meters--whatever) is right-angled, because a2 + b2 = 32 + 42 = 9 + 16 = 25 = c2 Ancient Egyptian builders may have known the (3,4,5) triangle and used it (with measured rods or strings) to construct right angles; even today builders may still nail together boards of those lengths to help align a corner. Many proofs exist and the easiest ones are probably the ones based on algebra, using the elementary identities discussed in the preceding section, namely 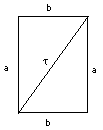
(a + b)2 = a2 + 2ab + b2 (recall that 2ab means 2 times a times b). For example
= 102 + (2)(10)(5) + 52 = 100 + 100 + 25 = 225 and (a - b) 2 = a2 - 2ab + b2 For example:
= 102 - (2)(10)(5) + 52 = 100 - 100 + 25 = 25 It is also necessary to know some simple areas: the area of a rectangle is (length) times (width), so the area of the one drawn above is ab. A diagonal cut divides it into two right-angled triangles with short sides a and b, and the area of such a triangle is therefore (1/2) ab. 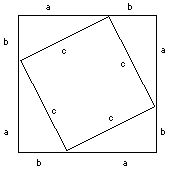
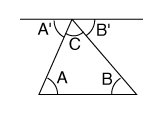
Now look at the square on the left constructed out of four (a,b,c) triangles. The length of each side is (a+b) and therefore the entire square has an area (a+b)2. However, the square can also be divided into four (a,b,c) triangles plus a square of side c in the middle (strictly speaking, we also ought to prove it is a square, but we will skip that). The area of each triangle, as shown earlier, is (1/2)ab, and the area of the square is c2. Since the big square is equal to the sum of all its parts (a + b) 2 = (4)(1/2)(a)(b) + c2 Using the identity for (a + b)2 and multiplying (4)(1/2) = 2 a2 + 2ab + b2 = 2ab + c2 Subtract 2ab from both sides and you are left with a2 + b2 = c2 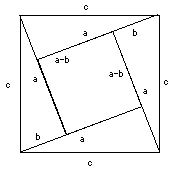
The same result can also be shown using a different square, of area c2. As the drawing on the right shows, that area can be divided into 4 triangles like the ones before, plus a small square of side (a-b). We get c2 = (4)(1/2)(a)(b) + (a-b) 2 = 2ab + (a2 - 2ab + b2) = a2 + b2 Q.E.D. Q.E.D. stands for "quod erat demonstrandum," Latin for "which was to be demonstrated," and in traditional geometry books those letters mark the end of a proof. The importance of the work of Pythagoras and of later masters of Greek geometry (especially Euclid) was not only in what they proved, but of the method they developed: start from some basic statements which are assumed to be valid ("axioms") and deduce by logic their more complicated consequences ("theorems"). Mathematics still follows the same pattern. |
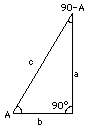
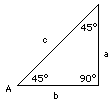 If A = 45°, then also (90° - A) = 45°, and therefore
If A = 45°, then also (90° - A) = 45°, and therefore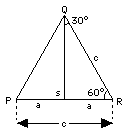 Consider the triangle PQR (drawing) with all three angles equal to 60°. By symmetry, all three sides are equal too (a more rigorous proof exists, but we skip it). Drop a line QS perpendicular to PR: it divides the big angle into two right-angled triangles with sharp angles of (30°, 60°), which is the kind we are interested in. By symmetry, the triangles are of equal size and shape ("congruent") and therefore (skipping another proof)
Consider the triangle PQR (drawing) with all three angles equal to 60°. By symmetry, all three sides are equal too (a more rigorous proof exists, but we skip it). Drop a line QS perpendicular to PR: it divides the big angle into two right-angled triangles with sharp angles of (30°, 60°), which is the kind we are interested in. By symmetry, the triangles are of equal size and shape ("congruent") and therefore (skipping another proof)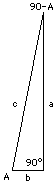 It would be rather hard to draw a right-angled triangle with a second angle of 90° inside it, because the third angle then has to be 0°. But we can visualize this strange triangle as the limiting case of long skinny triangles with an angle A that is very steep and and its complement (90° - A) very small (drawing). In the limiting case
It would be rather hard to draw a right-angled triangle with a second angle of 90° inside it, because the third angle then has to be 0°. But we can visualize this strange triangle as the limiting case of long skinny triangles with an angle A that is very steep and and its complement (90° - A) very small (drawing). In the limiting case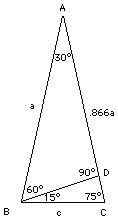
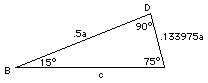 Now look at the triangle BDC: its two larger angles equal 90° and 75°, forcing the remaining angle to be equal to 15°. Using the theorem of Pythagoras, if the long side is denoted c, we get
Now look at the triangle BDC: its two larger angles equal 90° and 75°, forcing the remaining angle to be equal to 15°. Using the theorem of Pythagoras, if the long side is denoted c, we get
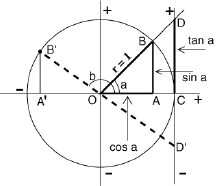
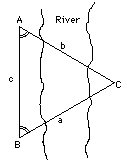
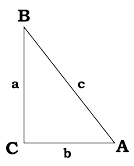 A triangle ABC has a right angle C and two sharp angles A and B. The triangle's sides AC and BC on both sides of the right angle C are given as:
A triangle ABC has a right angle C and two sharp angles A and B. The triangle's sides AC and BC on both sides of the right angle C are given as:
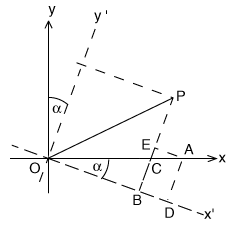
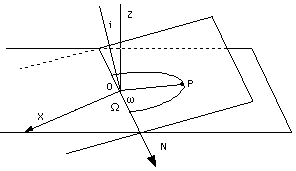 But what are its actual celestial coordinates (x,y,z)? From the illustration shown here (taken from section #12a), (x,y,z) can be reached by conducting two simple rotations by angles (w, i, W). To connect the two systems, the simple transformation derived above is applied, consecutively--first a rotation around line N by an angle i giving an intermediate system (x",y",z"), after which z' = z" = z. And then another rotation by an angle w+W around the shared z axis, bringing the x' axis, which originally passed the apogee P, into the celestial x axis.
But what are its actual celestial coordinates (x,y,z)? From the illustration shown here (taken from section #12a), (x,y,z) can be reached by conducting two simple rotations by angles (w, i, W). To connect the two systems, the simple transformation derived above is applied, consecutively--first a rotation around line N by an angle i giving an intermediate system (x",y",z"), after which z' = z" = z. And then another rotation by an angle w+W around the shared z axis, bringing the x' axis, which originally passed the apogee P, into the celestial x axis. A simple relation exists between this pair and the earlier ones. We have
A simple relation exists between this pair and the earlier ones. We have