Mapa del sitio

(8b) Paralaje

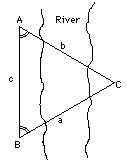
  "Pre-Trigonometría"

La Sección M-7 describe un problema básico de trigonometria (dibujo de la izquierda): encontrar la distancia a algún punto lejano C, dadas las direcciones a las que está C  desde dos  puntos de una línea base medida AB.
Este problema se hace algo más simple si: 
  1. La línea base es perpendicular a la línea desde su mitad al objeto, a fin de que el triángulo ABC sea simétrico. Designaremos sus lados por r:

    2. AC = BC = r 


  2. La longitud c de la línea base AB es mucho menor que r. Esto significa que el ángulo a entre AC y BC es pequeño; este ángulo se conoce como el paralaje de C, como se ve desde AB.

    3.  
  3. No pedimos una gran precisión, nos satisfaremos con un valor aproximado de la distancia, dentro del 1% de error.
El método presentado aquí ya era usado por los antiguos griegos hace más de 2000 años. Sabían que la longitud de una circunferencia de radio r era 2pr, donde p (que es una notación moderna, no usada por los griegos, aunque p seaparte de su alfabeto) simboliza un número algo mayor que, approximadamente:

p = 3.14159...

    (El matemático griego Arquímedes dedujo p con una precisión de cuatro decimales, aunque lo enunciaba de forma diferente, porque las fracciones decimales aparecen en Europa 1000 años más tarde.)
Dibuje un círculo alrededor del punto C, con radio r, pasando por A y B (dibujo superior). Dado  que el ángulo a es tan pequeño, la longitud de la línea recta b no es muy distinta del arco de circunferencia que pasa por A y B (dibujo de la derecha). Asumamos que las dos son iguales (esta es la aproximación hecha aquí). La longitud de un arco circular es proporcional al ángulo cubierto, luego
b cubre un ángulo a
2pr cubre un ángulo de 360°

tenemos

2p r = (360°/a) b 

y dividiendo por 2p

r = (360°/2pa) b

Por consiguiente, si conocemos b, podemos deducir r. Poe ejmplo, si sabemos que a = 5.73°, 2pa= 36°  y obtenemos

r = 10 b 

Calculando la distancia al aire libre

Es un método útil para excursionistas y scouts. Suponga que quiere calcular la distancia a un punto lejano, p.ej. edificio, árbol o aljibe elevado. 

El dibujo muestra una vista esquemática de la situación desde arriba (no a escala). Para calcular la distancia al punto A, haga lo siguiente:

 
The Thumb Method of Estimating Distances
  1.   Estire su brazo adelante y extienda su pulgar de tal forma que esté frente a sus ojos. Cierre un ojo (A') y mueva su pulgar de forma que su uña cubra la marca A.

    2.  
  2.   Ahora abra el ojo (A') y cierre el (B') sin mover su pulgar. Verá que lu uña de su pulgar está enfrente a otro lugar en el paisaje a casi la misma distancia que A, marcada B.

    3.  
  3.   Calcule la distancia AB, comparándola con las alturas de los árboles, anchura de edificios, distancias entre postes de luz, largo de los vehículos, etc,... La distancia a la marca es 10 veces la distancia AB. ¿Como es eso? Porque aún cuando las personas cambien de tamaño, las proporciones del cuerpo humano estandar son bastante constantes y para la mayoría de la gente la distancia  (A',B') al pulgar extendido es de unos 6°, bastante cercano al valor de 5.73° para el cual se encontró el ratio 1:10 anteriormente en esta sección.   Este ángulo es el paralaje de su pulgar, visto desde sus ojos. El triángulo A'B'C tiene las mismas proporciones que el triángulo mayor ABC y, por lo tanto, si la distancia B'C al pulgar es 10 veces la distancia A'B' entre los ojos, la distancia AC hasta la marca lejana es también de 10 veces la distancia AB. 

¿A que distancia está una Estrella?

    Cuando calculamos la distancia hasta un objeto muy distante, nuestra "línea base" entre los dos puntos de observación es mejor que sea grande también. Los objetos más distantes a nuestros ojos son las estrellas y están, efectivamente, muy lejos: la luz que se mueve a 300,000 km (186,000 millas) por segundo, necesitará años, a menudo muchos años, en alcanzarlas. La luz del Sol necesita 500 segundos en alcanzar la Tierra, un poco más de 8 minutos y unas 5.5 horas en alcanzar la distancia media a Plutón, el planeta más distante. Un "año luz" es unas 1600 veces más, una distancia enorme. 

      La mayor línea base disponible para medir tales distancias es el diámetro de la órbita de la Tierra, 300,000,000 kilómetros. El movimiento de la Tierra alrededor del Sol es de un lado a otro del espacio, de tal forma que en fechas separadas en medio año, sus posiciones están separadas 300,000,000 kilómetros. En adición, el sistema solar al completo también se mueve a través del espacio, pero ese movimiento no es periódico y por ello no se pueden separar sus efectos. 

      Y, ¿cuanto cambian las estrellas cuando se ven desde dos puntos separados 300,000,000 km?. Realmente muy poco. Durante muchos años los astrónomos lucharon en vano para observar la diferencia. Solo en 1838 se determinaron los paralajes medidos a algunas de las estrellas más cercanas,  Alfa Centauri por Henderson de Sudáfrica, Vega por Friedrich von Struve y  61 Cygni por Friedrich Bessel.

 Estas observaciones necesitan enorme precisión. En un círculo que está dividido en 360 grados (360º), cada grado está dividido en 60 minutos (60'), también llamados "minutos de arco" para distinguirlos de los minutos de tiempo y cada minuto contiene 60 segundos de arco (60''), todos los paralajes observados son menores de 1'', en el límite de resolución de los mayores telescopios terrestres.

Para medir las distancias a las estrellas, los astrónomos usan a menudo el pársec, la distancia a una estrella cuyo paralaje anual es 1''. Un pársec es igual a 3.26 años luz, pero, como ya se ha apuntado, no existe ninguna estrella tan cerca de nosotros. Alfa Centauri, la estrella del tipo solar más cercana a nuestro sistema solar, está a una distancia de 4.3 años luz y un paralaje de 0.75'' 

    Alfa Centauri no es un nombre, sino una denominación. Los astrónomos denominan las estrellas de cada constelación con letras del alfabeto griego: alfa, beta, gamma, delta y así sucesivamente, y "Alfa Centauri" indica la estrella más brillante de la constelación de Centauro, localizada alta en el cielo del sur. Necesita estar al sur del ecuador para verla bien. 
 

Página principal en Español (índice)


Linea del Tiempo               Glosario (English).

Próxima Etapa: #8c. ¿A que distancia está la Luna?--1

Author and Curator:   Dr. David P. Stern
     Messages to Dr.Stern:   stargaze("at" symbol)phy6.org   (English, please) .

Spanish translation by J. Guerrero

Last updated 13 December 2001