(Q-5) The Atomic Nucleus and

Bohr's Early Model of the Atom

then suggested a link between the frequencies of oscillation and the energies radiated.

    This neat picture was upset by a remarkable experiment performed in Manchester in 1909 by Ernest Rutherford, originally from New Zealand. It was known by then that heavy radioactive elements emitted "alpha particles" (α particles), fast ions of helium lacking both their electrons. That gave them a positive charge of +2e, twice the electron's charge of –e.

    Rutherford knew how to detect such ions individually. In total darkness, if they were allowed to hit a specially prepared fluorescent screen, the flash they produced was just bright enough to be seen by the dark-adapted eye, observing a small part of the screen through a microscope. The α particles were found to have enough energy to penetrate a thin gold foil, and Rutherford therefore set his assistant Hans Geiger (later assisted by Ernest Marsden) to examine how passage through such a foil affected their motion.

    With an atom resembling the one proposed by J.J. Thomson, the ions would feel no electric force while outside the gold atom, where effects of positive and negative charges cancelled. If they sliced through the edge of the atom, calculations suggested that the distributed positive electric charge would bend their path slightly.

    One quantity measured in joule-seconds was angular momentum.     That is a mechanical property (just as energy, say) of any rotating object or collection of objects--even of the Earth, Sun or the solar system. It measures the total "amount of rotation"--adjusted for the mass involved, its average distance from the axis of rotation, and of course, its rate of rotation. It is a vector quantity, its direction following the rotation axis.

    The rotations of Earth and Sun, and orbital motions of planets and moons, do involve angular momentum. A young Danish physicist named Niels Bohr, who arrived in England in 1912 and ended up working with Rutherford at the University of Cambridge, looked into the angular momentum of an electron orbiting a nucleus. It was guessed by then that as dimensions of a motion shrank to the atomic scale, Newton's laws were gradually modified, allowing electrons to have orbits where (for some yet-unknown reason) no energy was lost by broadcasting electromagnetic waves. Bohr went one step further: perhaps orbits were stable when the angular momentum of the motion equaled h times some whole number. In a large system, this might be millions of times larger than h, so the law allowed angular momentum (and energy) to change almost continuously. On the scale of a hydrogen atom, however, the possibilities were few, stable orbits were quite distinct, and so were their energy levels.

    For circular orbits in a hydrogen atom this worked beautifully, and also gave a consistent value of the Rydberg constant. Allowing the angular momentum to take values of nh/2π with n=1,2,3... gave orbits with energies which exactly matched Balmer's hydrogen spectrum (the factor 2π can be justified). A promising first step--but how to continue from here?

    Physical laws--the basic ones and those derived from them--usually make precise, quantitative statements, like F=ma, E=mc², E= hν. Very rarely does one encounter a law by which something is approximately true but not exactly (even though the approximation may be very good), e.g. valid for a long time but not to all eternity. Adiabatic invariance is of this kind.

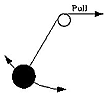
    Imagine a pendulum formed by a weight tied to a string, swinging back and forth under the influence of gravity. In each oscillation, as it descends to the bottom of its swing, it gains kinetic energy, then after having passed bottom, it slows down again, to stop briefly at the top of each swing. In the absence of friction and air resistance, one expects its total energy E (kinetic + potential) to stay unchanged, and the frequency ν and period T=1/ν of the oscillation will stay constant, too.

    If the string starts at a pulley (see drawing) and is slowly pulled up, the length of the pendulum will gradually decrease, and since a shorter pendulum has a higher frequency ν and a shorter period T, these quantities are also expected to change. But the energy E grows too, because extra work is being done against the force stretching the string, so the swing becomes more vigorous. Suppose the string is drawn up until its length is reduced by a certain fraction--say, by half. It can be shown that the change in the ratio E/ν can be made as small as we wish by making the drawing-up process slow enough.

    The ratio is not a real constant of the motion or "invariant" (like the energy in the undisturbed pendulum), but an approximate one, an "adiabatic invariant". The lack of constancy may be attributed to the fact that the tension in the string in any swing does not vary symmetrically--a small asymmetry is added by the fact the string is constantly being shortened, but slowing down the pull greatly reduces the asymmetry and its accumulated effects.

    Notice here that the adiabatic invariant E/ν has the same dimensions of joule-sec (i.e. same combination of measurable quantities--also called "action") as the elusive Planck's constant h.

    Adiabatic invariants occur in all sorts of periodic motions, including Kepler motion, which was taken as the model of the motion of an electron around the nucleus. Some physicists, notably Paul Ehrenfest, guessed that perhaps electron orbits were stable when the adiabatic invariant I of their motion equaled h times some whole number. For circular orbits in an atom, only one adiabatic invariant I existed, and allowing it to only take the values I=nh with n=1,2,3... gave orbits with energies which exactly matched Balmer's hydrogen spectrum.

    In the end it turned out that the quantization of angular momentum, rather than of I, gave a better qualitative understanding of atoms of more than one electron. That is discussed in the section that follows.