Site Map
Glossary
Timeline
Questions & Answers
Central Home Page


(34c) The L4 and L5 Lagrangian Points:
Alternative Derivation
    Index

28.Spaceflight
--------------------------

29. Spacecraft   (and 5 more)
-------------------

30.To Space by Cannon?

30a.Project HARP

31.Nuclear Spaceflight?

32. Solar Sails

32a. Early Warning of
        Solar Shocks

33. Ion Rockets

34.Orbits in Space

34a. L1 Lagrangian pt.

34b. L4/L5 Points (1)

34c.L4/L5 Points (2)

35. Gravity Assist

36. Pelton Turbine

        Afterword
The following derivation of the L4 and L5 points follows "When Trojans and Greeks Collide" by I. Vorobyov, "Quantum," p. 16-19, Sept-Oct. 1999. It is shorter, more elegant, more general, but requires some use of rotating frames of reference and of vectors.
    Note: Like the calculation is section (34b), this one too requires fluency in algebra. Trigonometry is not required, but vectors are used extensively. As with the other calculation, if you plan to study it, a good idea may be to copy it and check it out on paper as you go along.

Suppose we have 3 point-like masses (m1, m2, m3) orbiting under their mutual attraction. The three form a triangle ABC with sides masses (R1, R2, R3) where R1 is the side across from m1, R2 is across from m2 and R3 is across from m3 (Figure 1). We will assume that the motion starts out in the plane of that triangle, and since all forces are in that plane, too, it will stay there.

Is it possible for the three masses to keep all their mutual distances, keeping intact the shape of their triangle? Any such triangle must be rotating around some point O with constant period T. Let us see whether for any such motion all forces can be in equilibrium, which imply it was possible.

Let (r1, r2, r3) be the distances of the three masses from O. Their velocities are then

v1 = 2πr1/T         v2= 2πr2/T         v3 = 2 π 3/T

Rotating Frame of reference

All calculations from now on will be in a frame of reference rotating with the masses. In that frame, the triangle ABC is fixed and immovable, but in addition to gravitational attractions, each mass is also subject to a centrifugal force. The centrifugal forces are directed along (r1, r2, r3) are

m1v12/r1 = m1 (2π/T)2r1         m2v22/r2 = m2 (2π/T)2r2         m3v32/r3 = m3 (2π/T)2r3

The above three forces, directed outwards from O along (r1, r2, r3), must be included in any calculation of motion in the rotating frame. In a general derivation of forces in a rotating frame, Coriolis forces also enter. However, such forces only act on objects that move in the rotating frame, and since the masses keep fixed positions at the corners (A,B,C), such forces do not enter.

Vectors

It is now convenient to introduce vectors into the calculation--2-dimensional vectors in the plane of the triangle, distinguished by bold face lettering. The vectors r1, r2 and r3 are directed outwards from O, so the centrifugal forces are
m1(2π/T)2r1        m2(2π/T)2r2        m3(2π/T)2r3

Let the gravitational force on mass m1 from mass m2 by denoted F12, and on mass m2 from mass m1 by F21. If the masses are in equilibrium, in the rotating frame the total force on each is zero:

F12 + F13 + m1 (2π/T)2r1 = 0

F21 + F23 + m2 (2π/T)2r2 = 0

F32 + F31 + m3 (2π/)2 r3 = 0

Adding all equations

F12 + F13 + F21 + F23 + F32 + F31   +   (2π/T)2 [m1r1 + m2r2 + m3r3] = 0

However, by Newton's 3rd Law

F12 = –F21.
F13 = –F31.
F23 = –F32.

And therefore the sum of the 6 gravitational forces is zero, leaving

(2π/T)2 [m1r1 + m2r2 + m3r3] = 0

or
[m1r1 + m2r2 + m3r3] = 0

This can be shown to require the point O from which (r1, r2, r3)are measured to be the center of gravity of the three masses. It is no more than an extension of the assertion (section 25) that in a group of objects in which all forces are between one object and another (like the gravity between the masses here), the center of gravity stays fixed. (The same argument is easily extended to 4 or more objects.)

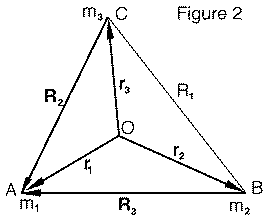
Useful Vector Relations

Next, let the sides (R2, R3) of the triangle be regarded as vectors (R2, R3), each directed towards m1 (Figure 2). Then using end-to-end vector addition

r1 = r2 + R3
r1 = r3 + R2
Also, obviously
r1 = r1         

Multiply the equations, in their order here, by m2, m3 and m1, and add:

r1 (m1 + m2 + m3) = [m2r2 + m3r3 + m1r1] + m3R2 + m2R3

However as shown earlier, the first sum on the right is zero (because O is the center of gravity). If we denoted the total mass by M

(m1 + m2 + m3) = M

then

M r1 = m3R2 + m2R3

We introduce two more vectors

ρ2 = R2 (m3/M)             ρ3 = R3 (m2/M)

with the same directions as (R2, R3). Then this becomes simply

r1= ρ2 + ρ3

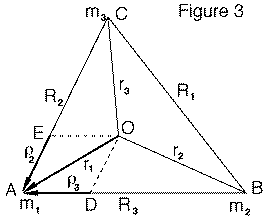We now interpret the above equation graphically. The vectors (ρ2, ρ3) have the same directions as (R2, R3), and can be represented by segments AE and AD in Figure 3. However, the equation

r1 = ρ2 + ρ3

and the properties of vector addition suggests that suggests that if AE represents ρ2, and we add to it a segment representing ρ3--parallel to AD and of the same length--then the end point will be the point O. (Or in other words, if a 4th point is added to (A,D,E) to form a parallelogram, that point will land on top of O.)

Now comes the trick!

The three forces on the mass m1--namely, F12, F13 and m1(2πT)2r1 --are all in equilibrium. Their vector sum must be zero, and therefore if we line them up end-to-end, they form a closed triangle.

The vectors are parallel to (R2, R3, r1), and therefore to (ρ3, ρ2, r1), so the triangle must be of the same shape as AEO and the lengths of its sides have the same proportions.

The length of a side of a triangle is the magnitude of the vector it represents. So

F12/F13 = ρ3/ρ2

Eliminating fractions by multiplying both sides by (F13ρ2) gives

F12 ρ2= F13 ρ3

Earlier it was shown that

ρ 2 = R2 (m3/M)
ρ3 = R3 (m2/M)

Also, by Newton's Law of gravitation, , if G is the "constant of gravitation"

F12 = G m1m2/R32
F13 = G m1m3/R22
Insert all these into the equation F12 ρ2 = F13ρ3 :

[G m1m2m3/M] R2/R32     =     [G m1m2m3/M] R3/R22

Dividing both sides by the square brackets

R2/R32 = R3/R22
and eliminating fractions by multiplying both sides by R22R32 finally gives

R33 = R23
which implies

R3 = R2

However, we might have gone through the same calculation with mass m2, involving sides R1 and R3 , which would have given R1 = R3. It follows that all three sides of the triangle ABC must be equal:

R1 = R2 = R3

If this holds, it is relatively easy to show that the 3 equations of equilibrium are satisfied, and given G, even to calculate T. The equilateral triangle ABC thus provides a true equilibrium.

Next Stop: #35 To the Planets, to the Stars

            Timeline                     Glossary                     Back to the Master List

Author and Curator:   Dr. David P. Stern
     Mail to Dr.Stern:   stargaze("at" symbol)phy6.org .

Last updated: 9-24-2004

Re-formatted 27 March 2006