|
Magnetic Fields Optional: Quantum Physics -------------------------- our Galactic Center of Atoms and Nuclei (first of 5 linked sections) |
. 2. Nuclear Binding EnergyA carbon nucleus of 12C (for instance) contains 6 protons and 6 neutrons. The protons are all positively charged and repel each other: they nevertheless stick together, showing the existence of another force--a nuclear attraction, "the strong nuclear force" which overcomes electric repulsion at very close range. Hardly any effect of this force is observed outside the nucleus, so it must have a much steeper dependence on distance--it is a short range force. The same force is also found to pull neutrons together, or bind neutrons and protons.The energy of the nucleus is negative (just like the energy of planets of the solar system--#7), for one must invest energy to tear a nucleus apart into its individual protons and neutrons (the energy is zero when all particles are independent). "Mass spectrometers" have actually measured the masses of nuclei, which are always less than the sum of the masses of protons and neutrons which form them, and the difference--by Einstein's famous E = mc2 --gives the binding energy of the nucleus. Nuclear Fusion |
|
The conversion of protons to neutrons is the result of another nuclear force, known as "the weak force" (the word "nuclear" is assumed here). The weak force also has a short range but is much weaker than the strong force. The weak force tries to make the number of neutrons and protons in the nucleus equal; these two particles are closely related and are sometimes collectively known as nucleons The protons combine to helium only if they have enough velocity to overcome each other's repulsion and get within range of the strong nuclear attraction, which means they must form a very hot gas. Hydrogen hot enough for combining to helium requires an enormous pressure to keep it confined, but suitable conditions exist in the central regions of the Sun ("core"), where such pressure is provided by the enormous weight of the layers above the core, created by the Sun's strong gravity. The process of combining protons to form helium is an example of nuclear fusion. Our oceans have plenty of hydrogen, and helium does not harm the environment, so it would be great if physicists could harness nuclear fusion to provide the world with energy. Experiments in that direction have so far come up short. Sufficiently hot hydrogen will also be ionized, and to confine it, very strong magnetic fields have been used, because charged particles (like those trapped in the Earth's radiation belt) are guided by magnetic field lines. Fusion experiments also rely on heavy hydrogen which fuses more easily, and gas densities have been kept moderate. In spite of all such tricks, though fusion energy has been released, so far more energy is consumed by the apparatus then is yielded by the process. The Curve of Binding EnergyIn the main isotopes of light nuclei, such as carbon, nitrogen and oxygen, the number of neutrons and of protons is indeed equal. However, as we move to heavier nuclei, the disruptive energy of protons increases, since they are confined to a tiny volume and repel each other. The energy of the strong force holding the nucleus together also increases, but at a slower rate, as if inside the nucleus, only nucleons close to each other are tightly bound, not ones more widely separated.
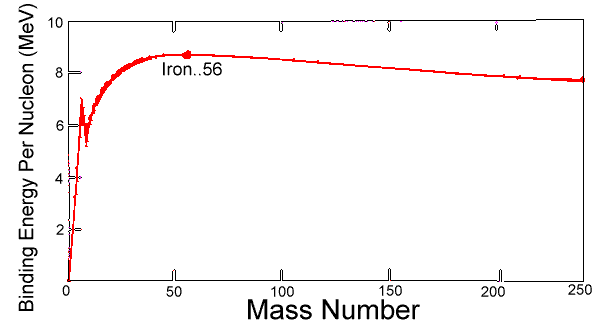
The net binding energy of a nucleus is that of the nuclear attraction, minus the disruptive energy of the electric force. As nuclei get heavier than helium, their net binding energy per nucleon (deduced from the difference in mass between the nucleus and the sum of masses of component nucleons) grows more and more slowly, reaching its peak at iron. As nucleons are added, the total nuclear binding energy always increases--but the total disruptive energy of electric forces (positive protons repelling other protons) also increases, and past iron, the second increase outweighs the first. One may say 56 Fe is the most efficiently bound nucleus.
To reduce the disruptive energy, the weak interaction allows the number of neutrons to exceed that of protons--for instance, in the main isotope of iron, 26 protons but 30 neutrons. Of course, isotopes also exist where the number of neutrons differs, but if these are too far from stability, after some time nucleons convert to a more stable isotope by beta emission radioactivity--protons turn into neutrons by dragging in an electron (or emitting a positron, the positive counterpart of the electron), or neutrons become protons by emitting electrons Among the heaviest nuclei, containing 200 or more nucleons, electric forces may be so destabilizing that entire chunks of the nucleus get ejected, usually in combinations of 2 protons and 2 neutrons ("alpha particles," actually fast helium nuclei) which are an extremely stable combination. The curve of binding energy (drawing) plots binding energy per nucleon against atomic mass. It has its main peak at iron and then slowly decreases again, and also a narrow isolated peak at helium, which as noted is very stable. The heaviest nuclei in nature, uranium 238U , are unstable, but having a lifetime of 4.5 billion years, close to the age of the Earth, they are still relatively abundant; they (and other nuclei heavier than iron) may have formed in a supernova explosion (reference #8) preceding the formation of the solar system. The most common isotope of thorium, 232T , also undergoes α particle emission, and its half-life (time over which half a number of atoms decays) is even longer, by several times. In each of these, radioactive decay produces "daughter isotopes" which are also unstable, starting a chain of decays which ends in some stable isotope of lead. Tidbit: The book "The Curve of Binding Energy" by John McPhee is actually the story of nuclear physicist Theodore Taylor and his diverse side-interests.Problems(answers in section S-8A-5)(1) Why can't one find in our environment elements whose atoms weigh 300 times as much as the proton, or more? (2) Compile a glossary, defining briefly in alphabetical order in your own words: Alpha radioactivity, Beta Radioactivity, Binding energy, Controlled nuclear fusion, Core of the Sun, Curve of binding energy, Daughter isotope, Deuterium, Mass spectrometer, Nuclear fusion Positron, Short range force, Strong (nuclear) force, Weak (nuclear) force, (3) What is the source of the Sun's energy? (4) Why is the binding energy of the nucleus given a negative sign? (5) (a) The atomic weight of deuterium (22 H) is 2.0140, of Helium 4 He 4.0026 (in units of the proton mass), and the "rest energy" E=mc2 of the proton is 938.3 MeV (million eV, with 1 eV = one electron-volt; see #9). How many eV are released when two atoms of deuterium combine to one of 4 He, by nuclear fusion?
(c) One gram of TNT can release 3.8 kilocalories of energy, each of which is equivalent to 4184 joules. How many tons of TNT are required to release the energy calculated above? The Sun loses mass all the time, by at least two mechanisms. First, it radiates sunlight energy E, and by the equivalence of energy and mass the process must also reduce its mass. The energy radiated at the Earth's orbit--150 million kilometers from the Sun--is about 1300 watt ("the solar constant") per square metre of area perpendicular to the Sun's rays, and the velocity of light is about c = 300,000 km/sec. Second, it also emits the solar wind. For reasons which after 70 years are still unclear, the uppermost atmosphere of the Sun ("solar corona") is very hot, about a million degrees centigrade, explaining why atoms in that layer tend to be stripped of most or all of their electrons--e.g. iron atoms missing a dozen electrons, which requires a tremendous amount of buffeting. The Sun's gravity cannot hold down a gas so hot. Instead, the topmost solar atmosphere is constantly blown away as the solar wind--a rarefied stream of free ions and electrons, moving outwards at about 400 km/second The density of that wind at the Earth's orbit is about 10 protons per cubic centimeter (taking into account the presence of helium ions), and the mass of a proton is about 1.673 10–27 kilograms. Which of the two processes causes the Sun a greater mass loss? (7) An object (e.g. a spaceship) ejected from the surface of Earth needs v1 = 11.3 km/s to escape Earth's gravity ("escape velocity"), A neutron has rest energy E0 = mc2 = 939.535 MeV (million electron volts). If the velocity of light is 300,000 km/sec (close enough) and a neutron is ejected from the Earth's surface with just enough velocity to escape gravity, what is its energy in MeV (or in electron volts, eV)? Use the non-relativistic expression when deriving the kinetic energy E1 of the escaping neutron (it is accurate enough). |
|
Timeline Glossary "From Stargazers to Starships" home page
Author and Curator: Dr. David P. Stern |