|
---------------------- Optional: Quantum Physics -------------------------- our Galactic Center of Atoms and Nuclei -------------------------- Spaceflight -------------------------- ------------------- |
Center of Gravity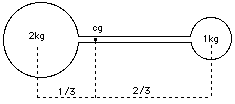
Most people have at least an intuitive notion of the center of gravity (CG) of an object: it is the point on which the object can be perfectly balanced. Grab a broom at one end and the other end tries to drop down; grab it at its center of gravity, and it stays balanced, neither end tipping over. If you have learned to balance a chair or a broom on the palm of your hand, you know the trick is to place your hand right below the center of gravity. Since your hand is not at the CG but below it, it must be constantly moved to keep that strategic position. There also exists a precise mathematical definition--it has nothing to do with gravity, which is why many scientists and engineers prefer the term center of mass. However, it leads off the main subject and therefore we won't bother with it now. A lightweight stick with two balls of equal weight at its end obviously has its CG in the middle. When one ball is twice the weight of the other, the CG divides the distance between them by a ratio 1:2, in a way that makes it closer to the heavier mass (see figure). And similarly for other ratios. Balls that push each other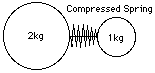
Now imagine that instead of a lightweight stick the above two heavy balls have a spring between them, held compressed by a string. Even though the balls are separate, one can speak of their common center of gravity, on the line connecting their centers, 1/3 of the distance from the center of the heavier ball. (The CG of the Earth-Moon system can be defined in the same manner. Since the ratio of masses of the two bodies is about 81:1, the CG is the point on the line between their centers dividing it by that ratio. It can be shown that--neglecting the pulls of the Sun and of other planets--the Moon does not orbit the center of Earth, but rather the common CG--and so does the Earth, reacting to the pull of the moon. Of course, since the Earth is much more massive, the CG is not very far from the center of the Earth--in fact, it is closer than the Earth's own surface.) Suppose next that a lit match is placed against the string, burning it through. As the spring expands, it pushes the balls apart; if it is sufficiently light, its own motion does not matter and we can assume that the balls push each other. |
|
By Mach's formulation of the equations of motion, if the heavy ball receives an acceleration a, then the light one gets 2a, twice as much. For each increment in the velocity of the heavy ball, the light one receives twice as much, and it follows that at any time, its total velocity, as well as the distance covered, are twice those of the heavy ball. Conservation of momentum leads to the same result. If then the heavy ball is at a distance D from the initial position of the spring, the light one is at distance 2D--as in the earlier figure, reproduced here. No matter how much time passes, the center of gravity stays at the same spot. RocketsThat turns out to be a very general principle: in any object or collection of objects, forces which only involve those objects and nothing else ("internal forces") cannot shift the center of gravity. An astronaut floating in a space suit cannot shift his position without involving something else, e.g. pushing against his spacecraft. The center of gravity--or "center of mass"--is a fixed point, which cannot be moved without outside help (turning around it, however, is possible). By throwing a heavy tool in one direction, the astronaut could get moving in the opposite direction, though the common center of gravity of the two would always stay the same. Given a bottle of compressed oxygen, the same result follows from squirting out a blast of gas (a scene that appeared in an early science fiction film). A rocket does much the same, except that the cold gas is replaced by the much faster jet of glowing gas produced by the burning of suitable fuel.
The powerful rockets which lift hundreds or even thousands of tons off the launching pad depend on the same principle. If you ever watched a rocket lift off at Cape Canaveral, it is worth remembering that if you could somehow remove from the scene the launching pad, the atmosphere and the Earth, then the combined center of gravity of the rocket and its exhaust gases would always remain where it started, at the launching point. It may seem like a round-about way for producing motion. And yet, rockets are (at least for now) the only practical means of leaving Earth and flying into space. --------------------------
Rocket MotionSuppose we have a rocket of total mass 2M, of which M is payload and M is fuel. As the fuel is burned, it is ejected with some constant velocity w relative to the rocket, creating (we assume) constant thrust. Let us simplify matters by also assuming the launch is from some point in space, so that the thrust of the engine only has to overcome the rocket's inertia. In launches from the ground, part of the thrust is needed to overcome gravity too--see Section #18.
But we need more! So we build a rocket of mass 4M, of which 2M is fuel, while the payload, also of mass 2M, is the smaller rocket described above, serving as second stage, with half of its mass also given to fuel (to simplify the calculation, we neglect the mass of the bigger rocket itself, although it, too, needs to be accelerated). When the fuel of the big rocket is finished, we reach a velocity V, then the second stage is ignited, adding another V to the velocity of the payload, for a total of 2V.
By now you can see the trend. If the mass of the final payload is M, then
Each time the velocity increases by one notch, the mass doubles.
However, Von Braun, leader of the US military rocket program, had provided a back-up plan, a 4-stage launcher capable of hurling a small scientific satellite into orbit. The first stage was a modified big "Redstone" missile, the second stage, a cylindrical cluster of 11 solid-fuel "Sergeant" rockets strapped together, the third stage 3 "Sergeants" strapped together (in the middle of the cylindrical cluster) and the fourth stage a single "Sergeant" which stayed attached to the payload. It worked, and the rest is history. 
Another problem of spaceflight is that big rockets cost big money. When using several stages, the first stage is the biggest and often the costliest. But it is also the one which attains the least speed, and therefore could perhaps be returned to Earth for re-use. The Space-X company of Elon Musk, which successfully produced economical space launchers, also developed a series of reusable first-stage rockets, capable of returning to Earth on their own and landing again on their tails (as the Apollo landers did). The initial flights started in 2011-2 with experimental craft of the " Grasshopper" series, and after some failures achieved success on 11 April 2016, landing the first stage of an orbital re-supply rocket on a remotely guided ship-platform. Before that (December 2015) it returned a first-stage rocket to land near its initial launching pad at Cape Canaveral, as shown here in a double-exposure photograph, combining both the launch and the first-stage landing. Also in 2016, the Blue Origin co. revealed and demonstrated its New Shepard reusable suborbital rocket, employing similar technology. Exploring Further: An article about scramjets, "Power for the Space Plane" by Thomas A. Jackson, Scientific American, August 2006, p. 56-63. Questions from Users: Why do rockets spin? *** The shapes of rockets and spacecraft. *** Stability during a rocket launch *** How can a spacecraft self-rotate? *** Launching a rocket from an airplane *** Reducing the fuel weight of the Space Shuttle? *** Barycenter of Earth-Moon system |
