|
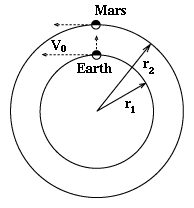
First, Earth's gravity will bend the trajectory of any spaceship launched from here. To remove that factor assume the rocket has already been placed in a distant orbit around Earth, where Earth's gravity is weak and orbital motion is slow, allowing both to be neglected. In actual orbit planning they must always be taken into account as a correction.
Even then, that rocket is still orbiting the Sun together together with the Earth, to which it is loosely attached, moving at close to 30 km/sec, a velocity we will write as V0. This is much faster than what is needed to reach the Mars orbit (or can be easily provided by rockets!). If we fire when Mars is closest (drawing), V0 is transverse to the aiming direction, so that the spaceship will start in a direction quite different from the one pointing at Mars--and Mars is sure to move away long before it has covered the intervening distance. That is the second reason.
The third reason is that the entire system is dominated by the Sun's gravity. All objects travel in orbits or trajectories, which by Kepler's laws are parts of conic sections--in this cases, ellipses. In general, these are curved.
Transfer Orbit
So instead of "aim and shoot," it is better search for an orbit which takes the spaceship from Earth to Mars, and to choose to launch when the arrival at the Mars orbit coincides with the arrival of Mars itself at the same location.
|
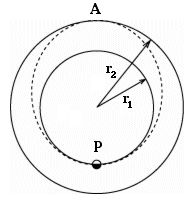
| The Hohmann Transfer Orbit
|
In addition, the direction in which the spaceship moves when it arrives should make it easy to match velocities with Mars. This leads to the so called Hohmann Transfer Ellipse (or transfer orbit), first proposed in 1925 by the German engineer Wolfgang Hohmann. That is an ellipse with perihelion P (point closest to the Sun) at the orbit of Earth and aphelion A (point most distant from the Sun) at the orbit of Mars (drawing). A similar transfer ellipse, between low Earth orbit (say, r = 1.1 RE = 1.1 Earth radii) and the synchronous orbit at 6.6 RE (see section #21a) is frequently used to inject communication satellites into their final orbits. We launch from P by giving the rocket an extra velocity in addition to V0, injecting it into the larger ellipse.
Mars should be in such a position relative to Earth at the time of launch, that it reaches point A at the same time as the spaceship does. To determine that position one needs to know the duration of the flight from P to A, and that is derived below, using Kepler's 3rd law.
Kepler's 3rd Law
Kepler's 3rd law as used here has the same form as in Section #10 . For completeness that form is re-derived below. The law states that for all objects orbiting the Sun
T2 / a3 = constant
where T is the orbital period and a the semi-major axis, half the length of the orbital ellipse (a=r in circular orbits). The constant is the same for all objects orbiting the Sun, including of course the Earth. Its exact value depends on the units in which T and a are measured.
That value becomes very simple if T is measured in years and a in AU (as is done here). Inserting in the 3rd-law equation the values for Earth gives
T = 1 (year) a = 1 (AU)
In our units, then
T2 / a3 = 1
Consequently in these units the constant also equals 1, and that value can be used for any planet. On multiplying both sides of the equation by a3 (second law of algebra)
T2 = a3
This again holds for any orbit around the Sun, including the one of a spaceship in a transfer ellipse. The length PA of that ellipse is, in AU,
r1 + r2 = 1 + 1.523691 = 2.523691 AU
That is the "major axis" of the orbital ellipse, and half its length equals the semi-major axis a. Therefore
a = 1.261845
a3 = 2.00918 = T2
Taking the square root
T = 1.417454 years
|
| Earth and Mars at launch
|
That is the time for going from P to A and back to P. The one-way transit time to Mars is half that, i.e.0.70873 years or about 8.5 months.
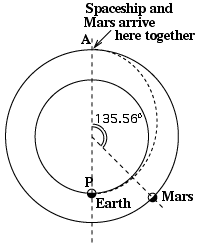
Location of Mars
Where should Mars be at the time of launch? From numbers cited at the beginning of this section, it takes Mars 1.8822 years for a full orbit of 3600. Therefore, assuming a circular orbit and uniform motion (a less accurate approximation for Mars than for Earth), in 0.70873 years it should cover
3600 * (0.70886 / 1.88) = 135.5550
We therefore launch when Mars in its orbit is 135.5550 away from point A (drawing)
The next section calculates the velocity which a rocket must impart at point P in order to produce the transfer orbit, and the velocity change required at point A to match velocities with Mars. That calculation is longer and requires some algebra.
|